Many fields use modeling and simulation to provide analysis and insight into building better systems, but the field of information protection has not produced significant research results in this area to date. Perhaps this is due to the extreme complexity of the cyber attack and defense problem, the enormous size of the search space, the lack of good data on attacks and defenses, the inability to derive consequences in a systematic way, or the lack of a coherent view of information protection. Despite these sometimes seemingly unscalable barriers, this paper is about simulations of attacks, defenses, and consequences in complex cyber systems such as computer networks; and more specifically about one attempt to create simulations capable of providing meaningful results in this field.
We begin by discussing limitations on modeling and simulation that are relatively unique to information protection, discuss the model we chose, and how simulation works. Next we show results of individual simulations and runs of a few thousand simulations that characterize small portions of the design space for attacks alone and then attacks in the presence of defenses. We continue with issues of parallel simulation and demonstrate results from large-scale simulation runs involving scores of parallel processors covering millions of runs and varying several parameters of interest. Results are given for the effects of detection and reaction time on success rates, the effects of defender strength on success rate, non-linearities between strength and time and the effectiveness of a defense, and differences between results for varying threat profiles. We then add issues of costs and produce expected loss and cost results, discuss and demonstrate the effects of strategies on results, review limitations of metrics and sensitivity to variations in parameters, and briefly discuss validation of results.
Modeling and simulation have been used in many fields for a variety of purposes, but the ultimate purpose of all such activity is, in one form or another, to gain experimental knowledge of events without performing experiments. Models are used to portray some specific issues in the systems under consideration and simulation is used to repeatedly exercise those models under different conditions. The limits of the value of modeling and simulation come from three things; (1) limits on accuracy of the models, (2) limits on the accuracy of the data upon which the simulation is based, and (3) the ability to explore the simulation space through the use of multiple runs of the simulator through the space.
In information protection, these three issues are often more complex than in many other fields. For example:
In a physics simulation, we pretty much know the nature of the physical phenomena under consideration and can model it at any desired level of granularity at the expense of increased computing power and decreased spatial size. Thus any number of reasonable models allows a particular granularity to be run with known accuracy in a given amount of time. While there may be factors that we are unaware of and therefore fail to include in our model, the model itself can be very close to perfect. In information protection, we are modeling very complex phenomena involving mixes of human behavior and interactions of complex interdependent systems with time bases ranging from nanoseconds to years. There is no widely published or accepted information physics which would allow us to make an accurate model, and the sizes of the things we are modeling are so large and complex that we cannot describe them with any reasonable degree of accuracy.
In most fields of science and engineering, we have measurable phenomena and we measure that phenomena as a preface to simulation. For example, in simulating a bridge, we know how large all the parts are, the properties of the materials, and so on. In information protection, we have no consensus on how to describe a protection system, and no set of commonly accepted metrics upon which to base a set of measurements to be used for simulation.
Runs through the information protection space are sequences of events that a number of different actors and automated systems may take. Depending on the precise order of events, dramatically different outcomes may result. There is no sense of localization or convergence. A small change in input may produce a large change in output. The most minor change in ordering could make the difference between an attack aborted almost as it begins and an attack which devastates an organization. This in turn means that a single missed run through the space may miss a major result - while the number of possible runs through the space is a power set of a large set of possibilities. The space it too large to explore and yet we cannot know how important a particular run will be to the outcome.
While this would seem to make the effort of developing simulations futile, it actually provides much of the best justification for actively pursuing it. Consider that a typical exercise of some set of minimal attacks against an information protection system costs tens of thousands of dollars. An attack that reflects what real people might actually do costs tens of thousands of dollars. In addition, these experimental attacks only provide one run through the space of possible scenarios. If the attack succeeds, it only indicates one path to the end, while if an attack fails, it only indicates that one attempt was thwarted. Furthermore, the cost associated with protection failure can be quite large. For many organizations, even a single attack can be devastating. The high cost of running real-world attacks, the limited extent to which they exercise the space of actual attacks, and the high potential for harm from a successful attack conspire to make some other means of analysis an imperative. The question is: What means do we use?
Many techniques have been used for trying to analyze information protection, from probabilistic risk analysis to a wide range of experience-based system analysis methods. While we don't universally dispute the value of these other techniques, they are limited in (1) their applicability, (2) their historical effectiveness, (3) their ability to help understand tradeoff issues encountered in real situations, and (4) their ability to model the effects of time and the sequential nature of attack and defense.
The limits of applicability are not known for the most part because of the lack of metrics and the lack of an overarching theory of information protection. The most experienced experts in this field have participated in in-depth analysis of at most several hundred organizations. Even the best experts cannot do a thorough analysis of a substantial organization in less than a few weeks of effort, which means that 20 organizations per year is the practical maximum experience of an individual. After 30 years in the field, this comes to less than 1,000 samples from which to judge by experience. Furthermore, the data from these analyses is not in a standard form and is not shared because of the contractual and legal limitations on revealing such information. Limits on probabilistic risk analysis and other similar methods comes from the disconnect between the underlying theory and the reality of the behavior of malicious actors in a rapidly evolving technology. There are something like a thousand new attack scripts published per year, and the probability of use changes on the scale of weeks to months. The actual loss often cannot be computed even after a loss has occurred, and the range of expected losses vary by several orders of magnitude depending on the specifics of what takes place. It has been described as an estimate multiplied by a guess computed to 3 digits of accuracy, and used to make multi-million dollar decisions. [Cohen97-03]
Data on the historical effectiveness of analysis techniques is not available, and it is not likely to becom available in the foreseeable future. One reason for this is that there is no repeatable experiment in real-world information protection. Each company that makes a decision simply lives with the result with no real way to measure the value of that decision. Analytical techniques such as probabilistic risk analysis can be applied, but the results are not of real value since the real events that transpire don't usually reflect the statistics upon which the analysis was based. Other less numerical methods are based on organizational or behavioral characteristics that reflect the practices of the most successful organizations, but they don't allow the analysis of tradeoffs. It is widely understood that the effectiveness of successful preventive defenses cannot be measured because you cannot tell what would have happened had they not been there. How can you measure what does not occur?
The ability to understand tradeoffs is severely limited in most methods of information protection analysis. For example, when we look at how an organization works in a qualitative way, we cannot analyze the effect of reducing our testing process in exchange for improving our training process. All we really know is that if you don't do both, you are asking for trouble, and if you do both, you can always do them better. We can tell you that you seem to be doing it better or worse, and if you have specific training and testing goals, we may be able to measure whether you meet them, but this is of no real value in determining how much to invest where or what the return on investment will be. In quantitative risk assessment, we can try to trade off different values for parameters, but the lack of measurement combined with the sensitivity of the results to minor changes in data values makes the value of the analysis highly dubious.
The real death blow to previous techniques is their inability to deal with the effects of time and the sequential nature of attack and defense in a meaningful manner. It is simply incongruous to try to understand the effectiveness of prevention of, detection of, and reaction to intentional acts of malicious, motivated, goal-directed actors without taking time into consideration. For example, what does the probability of success of an attack mean without a notion of how many times an attack can be attempted or the time taken per attempt? How can we hope to effectively model sequential attacks as parallel statistical events? How can we hope to determine how quickly we need to respond or the effect of response time when we don't include time in our models? But if we include the notion of time into these models, how can we evaluate the effects of time without analytical methods that model time? We cannot.
For the purposes of simulation, none of the previous models will do because they do not model anything that we can simulate. Furthermore, the previous models ignore the issue of time, which is fundamental to simulation. For this reason, we searched for other types of models.
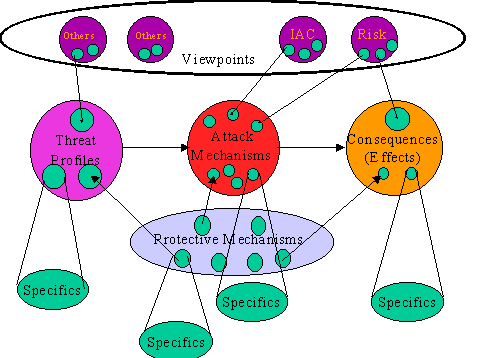
The models we examined were essentially schemes for classifying threats, attack mechanisms, protective mechanisms, and consequences. A reasonably good survey of these techniques is provided by John Howard in chapter 6 of his Ph.D. dissertation. [Howard97] The goal of our modeling process was to generate a set of cause-effect chains that would allow us to simulate the processes of attack and defense.
In the end, we designed our model with the notion of balancing complexity with the quality of the results. The complexity issue bears its head in two ways, (1) a simple model allows for very rapid simulation and a minimal number of parameters, but in exchange it collapses the problem into one that may be too simple to be meaningful, while (2) a fully detailed model of every specific threat, attack mechanism, and defense mechanism may be very accurate, but it requires massive amounts of data that are likely to change before any real system can be characterized and it will require enormous amounts of time in order to produce a meaningful characterization of the space. It is the tradeoff between specificity and performance that drove us to the model we use. To make this point a bit clearer, let's quickly look at two other extremes in modeling:
Suppose we take a very simple model such as the one used by Howard in his dissertation. While we don't intend to imply that the model is not useful for the purpose it was intended to be used for, its use in a simulation would leave us with severe limitations. Here is the scheme proposed by Dr. Howard:
The first problem we see in Table 1 is that all paths lead through one of two classes of vulnerability, three steps of unauthorized access, and corruption, denial, theft, or access. If we use this model, it brings almost no information about what protective measures might be effective, allows no differentiation between methods of attack and the time or effort they require, and leaves out the details that might lead to better design decisions. The tools in this model are strictly technical in nature, and thus the model misses the broad range of issues in information protection. Similarly, the number of threats are so few that a meaningful association of the threats with their methods is not attainable. This model was never intended to be used for the purpose of simulation, and as a result, it is not very useful in that application.
In Table 2, we have another example in which actors of different sorts use mechanisms of different sorts. Again we see too little complexity, but we do see an association between actors and actions that was missing in Howard's effort and this allows us to differentiate causes based on effects and effects based on causes to some extent. [Amo94] For example, if we have a case of physical destruction, the only possible causes are operators, and data entry clerks can only cause data diddling.
| Operators | Programmers | Data Entry | Internal | Outside | Intruders | |
|---|---|---|---|---|---|---|
| Physical Destruction | Bombing Short circuits |
|||||
| Information Destruction | Erasing Disks | Malicious software | Malicious software | Via modem | ||
| Data Diddling | Malicious software | False data entry | ||||
| Theft of Services | Theft as user | Unauthorized action | Via modem | |||
| Browsing | Theft of media | Unauthorized access | Via modem | |||
| Theft of Information | Unauthorized access | Via modem |
Another still different taxonomy (Table 3) exemplifies the use of a classification scheme to differentiate attack methods. While this scheme is not nearly filled out, it provides interesting detail that would be useful if it was fully described. [Landwehr94] While the resolution here is a bit better, this model lacks cause and effect relationships, notions of time, and so forth.
| ||||
At the other extreme, we have the notion of characterizing every known vulnerability in every system based on its configuration, every known attack method, and every configuration of prevention, detection, and reaction. To give a sense of this, there are more than 15,000 known computer viruses, scores of virus detection products, and it takes a substantial amount of effort to test any one version of any one product against the set of viruses. Simply analyzing the number of runs of 10 virus infections in the presence of a known scanner would lead to more than 10^40 possible runs, and the information gained would be of almost no value in determining, for example, how quickly to react to a virus attack, and much less valuable in assessing the potential for actual harm, which is largely unrelated to these details.
In the end, we chose a model of our own devising. (see Plate 1) The key issue underlying this decision was the notion that we need a basis for a cause-effect analysis of chains of events that can be overlaid on the architecture of an information environment. Once we have a model of cause and effect, we can begin to try to simulate, with the notion of time naturally falling out of the delay between cause and effect. The model we developed [Cohen98] was designed for the purpose of simulation and analysis and has been the subject of considerable research. It is based on a set of 37 classes of threats, 94 classes of attack mechanisms, and about 140 classes of protective mechanisms. These are interlinked by a database which associates threats with attacks and attacks with defenses. In addition, the database associates threats, attack methods and defense methods with other characteristics such as their impact on integrity, availability, access, and leakage; the sophistication level of the attackers; and their use in prevention, detection, and reaction.

This set of cross reference data provides a great deal of information which can be used in simulation, and is something that other models available today largely lack. This set of cross references comprises about 15,000 pieces of relational data. In addition to the pre-existing data, for the purposes of simulation we had to add about 20,000 new pieces of data to provide metrics which permit simulation to proceed in a meaningful manner. In particular, we needed to characterize the time required for each attack and each defense to operate and the effectiveness of each defense against each attack. These are also affected by attacker and defender skill levels. All of this is modeled by a set of statistical functions that provide results with the proper statistical characteristics whenever a value is called for by the simulator.
A large portion of these values are identical or similar to each other because they are a result of the way in which an organization operates. For example, reaction time for most detected security events is dominated by the incident response capability of the organization. It may take hours or even days before a detected attack generates a reaction that would result in defeating the attacker, regardless of the specific mechanisms, and with a few exceptions where automation has been chosen.
Values that are not tied to common phenomena tend to remain the same across many similar systems. For example, the likelihood that a virus scanner will detect a virus doesn't have to be experimentally derived for each system, and published results are available for most commercial products. Similarly, the prevention, detection, and reaction capabilities of a particular operating environment tend to be fixed by the system's design and augmented by add-on products. Once these have been characterized the first time, simply determining the system configuration yields most of the numerical values required for simulation. Some of these characteristics are described in a recent related paper. [Cohen9903]
Financial values are necessarily tied to the organization under study, as are network topologies, but again these can be greatly simplified by effective modeling to dramatically reduce data requirements. For example, most networks consisting of a firewall and a few hundred computers can be modeled effectively by five or six nodes for the purposes of understanding the process of attack and defense. A LAN consisting of 40 Windows computers, a Novel file server, and a Unix-based firewall might be modeled with only 4 nodes. Adding more nodes doesn't alter the result significantly, it only adds more complexity and data to the simulation.
To quickly summarize, we decided to model systems at a level that we felt would be meaningful in terms of the decisions that have to be made. This means that the model is limited in accuracy, but that it is feasible to explore the space and look at variations in parameters. More detailed models can be built, but the expense of doing so and the time required for such an activity is rarely justified. Even with the model we have selected, the specifics must be modified for each analysis done and there are significant data and computational requirements.
The simulation is driven by a model of the network under analysis, a cause and effect model of threats, attacks, and defenses, a set of characteristic functions that produce numerical values, and a pseudo-random number generator.
The network model consists of a set of nodes and links that describe the systems under attack.
The cause and effect model is the one described earlier and shown in Plat 1..
The characteristic functions that produce numerical values are generated by a team of analysts for each network under consideration. This is also called, in the parlance of war gaming, a firing table.
The pseudo-random number generator is, essentially, a linear feedback shift register. The results of this generation process is referred to in this paper, as in the parlance of war gaming, as dice rolls.
Simulation proceeds as follows:
The analysts program in the characteristic functions and model.
The user specifies a defender strength, strategy, and a number of simulation runs to be made involving a threat attempting to launch an attack starting at one node in the model and aimed at gaining access to another node in the model. Additional parameters may be added to reflect the form of the output and other related information.
The system computes a list of relevant attack methods and a set of feasible attack paths. The attack methods are chosen based on the capabilities of the selected threat(s) and any strategic information provided to guide the attack selection process. The feasible attack paths are generated by taking calculating all sequences of nodes that form non-looping paths from the source to the destination.
For each simulation run, pseudo-random values are used to select a specific attack path out of the feasible attack paths, to select each attack in turn based on the specified strategy, and to evaluate the performance of each attack, prevention, detection, and reaction. Each event that occurs is placed in an event queue in time order, with events capable of generating further events depending on the specifics of the outcomes. The next pending event is analyzed, the event queue is updated, and this continues until the attacker wins, the defender wins, or a maximum simulation time is exceeded.
For the purposes of the simulation runs we describe throughout this paper, the following diagram characterises the network. In this diagram, arrows indicate uni-directional information flow. Named nodes are linked with lines and defenses in each node are as specified in the listing.
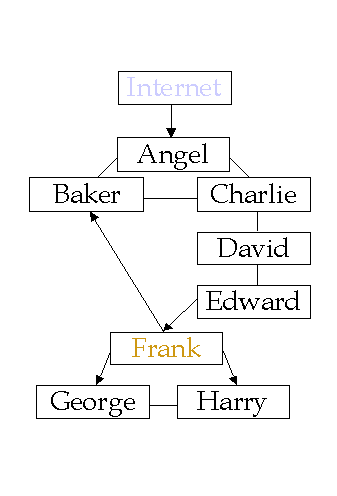
| Internet has no defenses Angel has anomaly detection, path diversity, sensors, waste data
destruction reintegration, improved morality, fine-grained access
control, perception management, integration principle, time, location,
function, and other similar access limitations, security marking and/or
labeling, auditing, and testing. Baker has fine-grained access control and perception management. Charlie has background checks, feeding false information, effective
mandatory access control, automated protection checkers and setters, and
trusted applications. David has time, location, function, and other similar access
limitations, auditing, and uninterruptable power supplies and motor
generators. Edward has program change logs, trusted applications, and effective
mandatory access control. Frank has properly prioritized resource usage, trusted system
technologies, and uninterruptable power supplies and motor generators. George and Harry have no defenses. |
The run in table 4 demonstrates the simulation process. The attacker is of type 10 (i.e., a hacker) who starts by trying to get into the Internet somewhere, and from there tries to attack Frank. The defender in this case acts correctly 90 percent of the time. Comments have also been added to this output for reader clarity.
In this table, What indicates attack,
defense, or comment; Node indicates the node involved;
Time indicates the time from the beginning of the attack in
years, months, days, hours, minutes, and seconds; What indicates
the technique used and whether it succeeds or fails; and Details
indicate the specifics of what happened. Specifics include [attacker
luck vs. defender quality] and, optionally, (luck relative to a
threshold).
(simulate '(10) "Internet" "Frank" 90)
| What | Node | Time | What | details | |
|---|---|---|---|---|---|
| ATTACK | Internet | below-threshold attacks->Internet | [743 !< 0](14 < 20) =======> Prevention will fail | ||
| COMMENT | The attacker stays below detection thresholds to get access to the Internet - This will succeed and take about 12 hours for this quality of attacker. | ||||
| ATTACK | Angel | 12h | process bypassing->Angel prevented | [527 < 900] by ((improved morality) (testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 13h | imperfect daemon exploits->Angel prevented | [227 < 895] by ((testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 13h 1m | breaking key management systems->Angel prevented | [471 < 883] by ((security marking and/or labeling) (time, location, function, and other similar access limitations) (waste data destruction)) | |
| COMMENT | Angel's prevention defeated the above attempts at entry | ||||
| ATTACK | Angel | 2d 13h 1m | race conditions->Angel | [964 !< 855](48 > 20) -> bad luck | |
| COMMENT | Angel was not able to prevent this attack, but the attacker was unlucky and what they tried failed | ||||
| ATTACK | Angel | 2d 13h 2m | below-threshold attacks->Angel prevented | [232 < 855] by ((perception management) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 3d 1h 2m | Trojan horses->Angel prevented | [627 < 900] by ((fine-grained access control) (improved morality) (testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 3d 1h 2m 30s | privileged program misuse->Angel prevented | [683 < 855] by ((perception management) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 3d 1h 3m 30s | false updates->Angel prevented | [514 < 900] by ((path diversity) (security marking and/or labeling) (testing) (time, location, function, and other similar access limitations)) | |
| COMMENT | False updates take a long time to get to work, whether they succeed or not. | ||||
| ATTACK | Angel | 33d 1h 3m 30s | shoulder surfing->Angel prevented | [36 < 895] by ((testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 33d 1h 13m 30s | shoulder surfing->Angel prevented | [101 < 895] by ((testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 33d 1h 23m 30s | infrastructure observation->Angel | [907 !< 866](21 > 20) -> bad luck | |
| ATTACK | Angel | 33d 1h 23m 40s | input overflow->Angel prevented | [40 < 895] by ((testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 33d 1h 23m 50s | error-induced mis-operation->Angel prevented | [513 < 855] by ((integration principle (GASSP)) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 33d 1h 43m 50s | call forwarding fakery->Angel prevented | [630 < 895] by ((testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 33d 1h 44m 50s | hardware failure - system flaw exploitation->Angel | [776 !< 765](55 > 20) -> bad luck | |
| COMMENT | Hardware failures only happen so often, again a long time is required. | ||||
| ATTACK | Angel | 63d 1h 44m 50s | illegal value insertion->Angel prevented | [457 < 889] by ((fine-grained access control) (testing)) | |
| ATTACK | Angel | 63d 1h 45m | shoulder surfing->Angel prevented | [554 < 895] by ((testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 63d 1h 55m | shoulder surfing->Angel prevented | [560 < 895] by ((testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 63d 2h 5m | perception management a.k.a. human engineering->Angel prevented | [450 < 898] by ((perception management) (testing) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 73d 2h 5m | implied trust exploitation->Angel prevented | [190 < 855] by ((testing)) | |
| ATTACK | Angel | 73d 2h 6m | replay attacks->Angel prevented | [272 < 810] by ((time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 73d 2h 16m | below-threshold attacks->Angel prevented | [99 < 855] by ((perception management) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 73d 14h 16m | cryptanalysis->Angel prevented | [23 < 810] by ((time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 73d 15h 16m | dumpster diving->Angel | [868 !< 675](2 < 20) =======> Prevention will fail | |
| COMMENT | Angel will be defeated by information gained in dumpster diving. It has taken 73 days to get through | ||||
| ATTACK | Charlie | 73d 19h 16m | cryptanalysis->Charlie | [404 !< 0](19 < 20) =======> Prevention will fail | |
| COMMENT | Charlie falls right away. | ||||
| ATTACK | David | 73d 20h 16m | undocumented or unknown function exploitation->David prevented | [771 < 810] by ((time, location, function, and other similar access limitations)) | |
| ATTACK | David | 73d 20h 16m 10s | viruses->David | [155 !< 0](85 > 20) -> bad luck | |
| ATTACK | David | 73d 20h 46m 10s | strategic or tactical deceptions->David | [413 !< 0](63 > 20) -> bad luck | |
| ATTACK | David | 74d 20h 46m 10s | shoulder surfing->David | [844 !< 810](50 > 20) -> bad luck | |
| ATTACK | David | 74d 20h 56m 10s | error-induced mis-operation->David prevented | [510 < 810] by ((time, location, function, and other similar access limitations)) | |
| ATTACK | David | 74d 21h 16m 10s | illegal value insertion->David | [583 !< 0](18 < 20) =======> Prevention will fail | |
| COMMENT | David has some successful prevention and the attacker had some bad luck, but it didn't take long to get through. | ||||
| ATTACK | Edward | 74d 21h 16m 20s | invalid values on calls->Edward | [398 !< 0](89 > 20) -> bad luck | |
| ATTACK | Edward | 74d 21h 16m 30s | infrastructure observation->Edward | [704 !< 0](67 > 20) -> bad luck | |
| ATTACK | Edward | 74d 21h 16m 40s | viruses->Edward prevented | [664 < 898] by ((effective mandatory access control) (trusted applications)) | |
| ATTACK | Edward | 74d 21h 46m 40s | process bypassing->Edward prevented | [819 < 855] by ((trusted applications)) | |
| ATTACK | Edward | 74d 22h 46m 40s | imperfect daemon exploits->Edward prevented | [848 < 898] by ((effective mandatory access control) (trusted applications)) | |
| ATTACK | Edward | 74d 22h 47m 40s | Trojan horses->Edward | [964 !< 898](24 > 20) -> bad luck | |
| ATTACK | Edward | 74d 22h 48m 10s | hardware failure - system flaw exploitation->Edward | [987 !< 0](78 > 20) -> bad luck | |
| ATTACK | Edward | 104d 22h 48m 10s | strategic or tactical deceptions->Edward | [983 !< 0](25 > 20) -> bad luck | |
| ATTACK | Edward | 105d 22h 48m 10s | shoulder surfing->Edward | [468 !< 0](51 > 20) -> bad luck | |
| ATTACK | Edward | 105d 22h 58m 10s | cryptanalysis->Edward | [639 !< 0](94 > 20) -> bad luck | |
| ATTACK | Edward | 105d 23h 58m 10s | implied trust exploitation->Edward prevented | [117 < 855] by ((trusted applications)) | |
| ATTACK | Edward | 105d 23h 59m 10s | collaborative misuse->Edward | [426 !< 0](17 < 20) =======> Prevention will fail | |
| COMMENT | Edward had better defenses for this threat profile and luck was not with the attacker. | ||||
| ATTACK | Frank | 106d 59m 10s | hardware failure - system flaw exploitation->Frank | [575 !< 0](18 < 20) =======> Prevention will fail | |
| COMMENT | Frank, however, fell after one very well directed and time consuming attack. | ||||
| A WINS | Frank | 136d 59m 10s | =======> | Defeated Frank |
Large numbers of simulation runs may be made with
the same parameter values to generate statistics. This result of
running the same attacker / defender pairing is demonstrated in the
detailed run through 1,000 attack sequences given in table 5.
(simset '(10) "Internet" "Frank" 90 1000) Run time: 1065.85 sec.
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 1d 17h 12m 10s | 2yr 77d 15h 52m 40s | 1000 | 210d 7h 25m 50s | 7d 16h 59m 28s |
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 1d 17h 12m 10s | 81d 17h 35m | 101 | 54d 14h 53m 8s | 5d 20h 5m 38s |
| 82d 12h 15m 40s | 162d 17h 30m 20s | 309 | 123d 13h 52m 56s | 7d 3h 39m 18s |
| 163d 19m 30s | 243d 11h 43m 30s | 273 | 199d 7h 40m 10s | 12d 3h 24m 8s |
| 243d 13h 17m | 321d 21h 57m 20s | 153 | 277d 12h 42m 7s | 22d 12h 16m 59s |
| 324d 11h 25m 10s | 1yr 39d 15h 19m 40s | 93 | 357d 17h 42m 24s | 37d 4h 5m 23s |
| 1yr 40d 10h 25m 50s | 1yr 117d 20h 38m | 34 | 1yr 75d 5h 41m 50s | 75d 14h 31m 12s |
| 1yr 122d 17h 43m 10s | 1yr 195d 11h 53m 30s | 20 | 1yr 153d 18h 53m 44s | 116d 2h 34m 23s |
| 1yr 201d 8h 48m 20s | 1yr 278d 5h 38m 50s | 10 | 1yr 232d 23h 49m 32s | 189d 7h 21m 26s |
| 1yr 291d 8h 44m 50s | 1yr 340d 50m 10s | 4 | 1yr 317d 22h 5m 25s | 341d 14h 1m 48s |
| 2yr 63d 5h 50m 40s | 2yr 77d 15h 52m 40s | 3 | 2yr 71d 23h 48m 53s | 1yr 98d 1h 4m 16s |
| From | To | Samples | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1d 17h 12m 10s | 81d 17h 35m | 101 | XX | XX | XX | XX | XX | XX | ||||||||||||||
| 82d 12h 15m 40s | 162d 17h 30m 20s | 309 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |
| 163d 19m 30s | 243d 11h 43m 30s | 273 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |||
| 243d 13h 17m | 321d 21h 57m 20s | 153 | XX | XX | XX | XX | XX | XX | XX | XX | XX | |||||||||||
| 324d 11h 25m 10s | 1yr 39d 15h 19m 40s | 93 | XX | XX | XX | XX | XX | |||||||||||||||
| 1yr 40d 10h 25m 50s | 1yr 117d 20h 38m | 34 | XX | XX | ||||||||||||||||||
| 1yr 122d 17h 43m 10s | 1yr 195d 11h 53m 30s | 20 | XX | |||||||||||||||||||
| 1yr 201d 8h 48m 20s | 1yr 278d 5h 38m 50s | 10 | ||||||||||||||||||||
| 1yr 291d 8h 44m 50s | 1yr 340d 50m 10s | 4 | ||||||||||||||||||||
| 2yr 63d 5h 50m 40s | 2yr 77d 15h 52m 40s | 3 |
The runs in table 5 show statistical characteristics
that look like a Bell-curve, but, this is not generally the case for
attack and defense simulations. This particular example is unlikely to
produce high variance because the set of attack capabilities and
defender strength are balanced in a particular way. It is also common
to have curves like the one in table 6:
(simset '(34) "Internet" "Frank" 20 1000) Run time: 143.99 sec.
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 1h | 70d 10h 55m | 1000 | 13d 17h 31m 54s | 13h 39m 41s |
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 1h | 23h 35m | 264 | 7h 38m 55s | 32m 17s |
| Empty Interval | ||||
| 10d 1h | 10d 14h 25m | 327 | 10d 6h 40m 10s | 13h 38m 32s |
| 10d 14h 30m | 10d 23h 20m | 18 | 10d 18h 15m 33s | 2d 12h 52m 31s |
| Empty Interval | ||||
| 20d 40m | 21d 3h 20m | 240 | 20d 7h 29m 46s | 1d 7h 28m 9s |
| Empty Interval | ||||
| Empty Interval | ||||
| 30d 30m | 31d 45m | 103 | 30d 7h 29m 10s | 2d 23h 40m 57s |
| Empty Interval | ||||
| Empty Interval | ||||
| 40d 50m | 40d 17h 45m | 37 | 40d 7h 23m 30s | 6d 15h 2m 22s |
| Empty Interval | ||||
| Empty Interval | ||||
| 50d 5m | 50d 14h 20m | 7 | 50d 7h 19m 17s | 19d 19m 42s |
| Empty Interval | ||||
| Empty Interval | ||||
| 60d 40m | 60d 9h 10m | 3 | 60d 5h 40m | 34d 18h 39m 31s |
| Empty Interval | ||||
| 70d 10h 55m | 70d 10h 55m | 1 | 70d 10h 55m | 70d 10h 55m |
| From | To | Samples | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1h | 23h 35m | 264 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 10d 1h | 10d 14h 25m | 327 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |
| 10d 14h 30m | 10d 23h 20m | 18 | XX | |||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 20d 40m | 21d 3h 20m | 240 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | ||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 30d 30m | 31d 45m | 103 | XX | XX | XX | XX | XX | XX | ||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 40d 50m | 40d 17h 45m | 37 | XX | XX | ||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 50d 5m | 50d 14h 20m | 7 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 60d 40m | 60d 9h 10m | 3 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 70d 10h 55m | 70d 10h 55m | 1 |
The example in table 6 has clusters of samples surrounding substantially different times and large areas (labeled Empty Interval) with no samples. We have used 20 intervals to make this clearer for this data set, but the same phenomena happens for most data sets at an appropriate level of granularity.
At first this was a great surprise. In fact, the authors' initial reaction was to disbelieve the simulation, so the details of the runs were examined to see what was wrong with the simulator. It turned out that the simulator was working properly and that simulation had revealed a new property of attacks.
This result turns out to be a side effect of the large time differential between different attack techniques. For example, getting a job in order to break into a site is something that a spy would commonly do while a hacker probably would not. For cases where a job is used as an entree, the time scale is on the order of weeks to months, and sometimes years, while most of the technical attacks operate in time scales of seconds to hours. Thus the distribution is very different when human and computer time scales are mixed. If a purely technical attack is going to work, it will usually work quickly. If a series of technical attacks fail and the attacker decides to use human effort, there is a relatively large gap. So the gaps in times reflect the numbers and sorts of human activities within the attack process as well as differentials associated with slower and faster technical attacks.
This example also has a very low-grade defender (only 20 percent of what they do is done right) and a relatively non-technical threat (a paramilitary group). While the curve in table 6 is generally similar to the one from table 5 in that it rises to a peak and then trails off slowly, the clustering has a substantial impact.
Table 6 covers 1,000 samples and 12 out of 20 equal-sized regions have no samples. In a similar run with a very high grade threat (information warriors) only 5 regions had data and, of those; one had 88 percent of results, the next highest had 8 percent, and the third highest had 3 percent. One of the interesting results is that the time clustering of successful attacks is reduced for higher quality defenders, but this tends to happen only as the quality becomes very nearly perfect.
It is also worth noting that the run time for simulation is dramatically affected by the strength of the attacker and defender. This essentially reflects the notion that better defenders force attackers to try more things before success and better attackers have to try fewer things before success. The real-time till success is also far shorter in this case for the same reasons. In the case of the stronger attacker and weaker defender, 14d 13m 44s was the mean time till success, while the stronger defender with the weaker attacker has a mean time to success of 210d 6h 51m 58s - a factor of about 15.
Another key issue that clustering points out is the notion of attack strategies. While these simulations use random selection to decide which attack of those available to the threat is picked next, an actual attacker's strategy might be very different. For example, some attackers may only use methods that they think are hard to detect, while others may go for pure speed, others may try a small number of attacks repeatedly until they succeed, others may tend to try attacks that succeeded well in previous attempts, and still others may choose quicker attacks with increased likelihood. Clearly, this has implications both for attackers and defenders in terms of understanding the issues of attack and defense, but just as clearly, the resources required to do this sort of analysis are considerable. We will address the issues of strategies and resources a bit later.
Another very important consideration in this case is the lack of detection and reaction in the model. In practice, only a very subtle attack will likely use a large number of steps and go undetected by a reasonable defender. Once detected, reaction, even on human time scales, may easily defeat the attack most of the time. Even the fastest success in the hacker runs shown in Table 5 (1d 12h 55m) is within the realm of what human reaction has a chance to stop.
This is not universally true, of course. Stronger attackers tend to gain entry far more quickly. For example, in a subsequent run, a simulated information warrior operating against a fully skilled defender was able to gain access to Frank in 4 minutes, 27 seconds. This is far faster than human defenders are likely to be able to react except in the rarest of circumstances.
This also brings up the issue of attacker and defender quality. We characterize this as a probabilistic measure that affects the firing tables and dice rolls. On each attack and defense, you can see thresholds for success both for the attacker and defender along with the numbers actually used in the particular move. These thresholds are varied based on the attacker and defender quality provided as input to the simulation. In the case of defenders, the quality is a simulation parameter, while threats have quantitative values in the database used to drive the simulation.
While these simulations provide interesting results, they ignore detection and reaction to attacks. One way to think of this is in terms of the rating of a physical firewall or a safe. These physical security devices are typically rated in terms of how long they can withstand what sort of assault. A 16-hour safe, for example, is designed to take 16 hours to penetrate given an identified safecracker capability. A 2-hour firewall or firesafe is rated based on the time it takes to bring the protected items up to a particular temperature given a particular temperature fire on the other side of the wall.
Effective protection works because of the
combination of prevention, detection, and reaction. Deterrence, arrest
and prosecution, and other factors also come into play in a strategic
sense, but for the time being, and for the purpose of our current
simulations, only tactical issues are considered. Results change rather
substantially when we include detection and reaction in the picture.
The first and most noticeable change is that all attacks do not
eventually succeed. With detection and reaction in place, a key
parameter of interest to many people is the probability of successful
attack. But this is only the beginning of the issue. Table 7 has an
example simulation in which detection and reaction has been included.
An industrial espionage expert is trying to get from the Internet to
Edward with the defender at 80 percent strength:
| What | Node | Time | What | details |
|---|---|---|---|---|
| ATTACK | Internet | spoofing and masquerading->Internet | [208 !< 0](12 < 57) =======> Prevention will fail | |
| DETECT | Angel | 1s | perception management a.k.a. human engineering->Angel detected | [125 < 768] by ((anomaly detection) (testing) (time, location, function, and other similar access limitations)) in 2h |
| ATTACK | Angel | 1s | perception management a.k.a. human engineering->Angel | [804 !< 798](86 > 57) -> bad luck |
| ATTACK | Angel | 1m 1s | collaborative misuse->Angel prevented | [98 < 794] by ((improved morality) (path diversity)) |
| DETECT | Angel | 11m 1s | get a job->Angel detected | [307 < 748] by ((sensors) (testing) (time, location, function, and other similar access limitations)) in 1h 20m 6s |
| ATTACK | Angel | 11m 1s | get a job->Angel prevented | [22 < 800] by ((path diversity) (testing) (time, location, function, and other similar access limitations) (waste data destruction)) |
| REACT- | Angel | 1h 31m 7s | get a job@ 11m 1s | [859 !< 584]=>((time, location, function, and other similar access limitations) (waste data destruction)) |
| REACT- | Angel | 2h 1s | perception management a.k.a. human engineering@ 1s | [950 !< 728]=>((perception management) (time, location, function, and other similar access limitations)) |
| DETECT | Angel | 28d 11m 1s | restoration process corruption or misuse->Angel detected | [111 < 787] by ((security marking and/or labeling) (testing) (time, location, function, and other similar access limitations)) in 2h |
| ATTACK | Angel | 28d 11m 1s | restoration process corruption or misuse->Angel prevented | [382 < 800] by ((path diversity) (security marking and/or labeling) (testing) (time, location, function, and other similar access limitations)) |
| ATTACK | Angel | 28d 41m 1s | repair-replace-remove information->Angel prevented | [293 < 790] by ((testing) (waste data destruction)) |
| REACT+ | Angel | 28d 2h 11m 1s | restoration process corruption or misuse@ 28d 11m 1s | [361 < 560]=> ((time, location, function, and other similar access limitations)) after 2h======> Reaction will succeed in 1d |
| ATTACK | Angel | 29d 41m 1s | collaborative misuse->Angel prevented | [575 < 794] by ((improved morality) (path diversity)) |
| DETECT | Angel | 29d 51m 1s | excess privilege exploitation->Angel detected | [34 < 793] by ((anomaly detection) (security marking and/or labeling) (testing) (time, location, function, and other similar access limitations)) in 2h |
| ATTACK | Angel | 29d 51m 1s | excess privilege exploitation->Angel | [887 !< 797](49 < 57) =======> Prevention will fail |
| ATTACK | Charlie | 29d 51m 2s | collaborative misuse->Charlie prevented | [628 < 760] by ((background checks) (feeding false information)) |
| ATTACK | Charlie | 29d 1h 1m 2s | inappropriate defaults->Charlie prevented | [699 < 770] by ((automated protection checkers and setters) (effective mandatory access control)) |
| ATTACK | Charlie | 29d 1h 1m 12s | resource availability manipulation->Charlie prevented | [673 < 799] by ((automated protection checkers and setters) (effective mandatory access control) (trusted applications)) |
| ATTACK | Charlie | 29d 1h 1m 13s | dumpster diving->Charlie | [249 !< 0](96 > 57) -> bad luck |
| ATTACK | Charlie | 29d 2h 1m 13s | protection mis-setting exploitation->Charlie | [816 !< 799](95 > 57) -> bad luck |
| ATTACK | Charlie | 29d 2h 2m 13s | modification in transit->Charlie | [926 !< 760](1 < 57) =======> Prevention will fail |
| ATTACK | David | 29d 2h 2m 14s | repair-replace-remove information->David | [848 !< 0](27 < 57) =======> Prevention will fail |
| D WINS | Angel | @ 29d 2h 11m 1s | Original Attack@ 28d 11m 1s Detected@ 28d 2h 11m 1s Reacted with:((time, location, function, and other similar access limitations)) after 1d |
At 1 second into the attack, the Internet has been breached and a perception management attack against Angel has been detected by a combination of anomaly detection, testing, and time, location, function, and other similar access limitations. It will take 2 hours before this detection reaches a person or system capable of considering a reaction. At 2 hours and 1 second into the attack, the perception management attempted at 1 second into the attack is not reacted to because of defender weakness, so the attack continues.
A restoration process corruption or misuse against Angel is detected at 28 days, 11 minutes and 1 second into the simulation by the combined defenses of security marking and/or labeling, testing, and time, location, function, and other similar access limitations. It will again take 2 hours before an actor capable of responding will get the alert, and at 28d 2h 11m 1s time, location, function, and other similar access limitations is chosen to block further attacks. It will take the organization 1 day to implement this protection, but at that time the attack will be defeated by this method. Sure enough, at 29d 2h 11m 1s into the simulation, the defender wins by this method.
Table 8 has another simulation run under identical
initial conditions, but the dice will roll differently this time.
| What | Node | Time | What | details | |
|---|---|---|---|---|---|
| ATTACK | Internet | network service and protocol attacks->Internet | [272 !< 0](80 > 57) -> bad luck | ||
| ATTACK | Internet | 1s | invalid values on calls->Internet | [274 !< 0](89 > 57) -> bad luck | |
| ATTACK | Internet | 2s | reflexive control->Internet | [116 !< 0](35 < 57) =======> Prevention will fail | |
| DETECT | Angel | 3s | modification in transit->Angel detected | [527 < 768] by ((anomaly detection) (sensors) (time, location, function, and other similar access limitations)) in 1h 20m 6s | |
| ATTACK | Angel | 3s | modification in transit->Angel prevented | [444 < 788] by ((path diversity) (time, location, function, and other similar access limitations)) | |
| ATTACK | Angel | 4s | input overflow->Angel | [841 !< 796](56 < 57) =======> Prevention will fail | |
| ATTACK | Charlie | 5s | modeling mismatches->Charlie prevented | [524 < 720] by ((feeding false information)) | |
| ATTACK | Charlie | 15s | wire closet attacks->Charlie | [155 !< 0](30 < 57) =======> Prevention will fail | |
| DETECT | David | 1m 15s | excess privilege exploitation->David detected | [93 < 720] by ((time, location, function, and other similar access limitations)) in 2h | |
| ATTACK | David | 1m 15s | excess privilege exploitation->David prevented | [52 < 720] by ((time, location, function, and other similar access limitations)) | |
| DETECT | David | 1m 16s | excess privilege exploitation->David detected | [256 < 720] by ((time, location, function, and other similar access limitations)) in 2h | |
| ATTACK | David | 1m 16s | excess privilege exploitation->David | [867 !< 720](5 < 57) =======> Prevention will fail | |
| ATTACK | Edward | 1m 17s | spoofing and masquerading->Edward | [439 !< 0](42 < 57) =======> Prevention will fail | |
| A WINS | Edward | 1m 18s | =======> | Defeated Edward |
In this case, the attacker was detected after only 3 seconds when trying to modify data in transit. The detection was accomplished by the combination of anomaly detection, sensors, and time, location, function, and other similar access limitations, and a person or system capable of responding will be alerted in only 1h 20m 6s. Unfortunately, at 1m 18s into the attack, the attacker broke through to the target - long before reaction could even be contemplated. This clearly shows a case where automated reaction might be effective but human reaction would likely fail, even if it were quite rapid. Detection and reaction times are highly technique and organization dependent and are parameters in the firing tables. As we can see, they also have a substantial impact on the effectiveness of defense.
When we look at substantial numbers of simulation
runs with detection and reaction included in the process, we get results
like those shown in Table 9. This has the same parameters as the runs
plotted in Table 6, but with detection and reaction included. We plot
successful attacks in red and successful defenses in green.
(simset '(34) "Internet" "Frank" 20 1000) Run time: 144.95 sec.
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 55m | 70d 5h 15m | 966 | 13d 23h 38m 48s | 14h 9m 56s |
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 55m | 22h 50m | 256 | 7h 45m 1s | 33m 21s |
| 10d 50m | 11d 2h 25m | 330 | 10d 7h 56m 1s | 13h 39m 3s |
| 20d 40m | 20d 21h 55m | 216 | 20d 7h 21m 5s | 1d 9h 9m 41s |
| Empty Interval | ||||
| 30d 35m | 30d 22h 40m | 111 | 30d 7h 35m 32s | 2d 21h 3m 41s |
| 40d 1h | 41d 2h 10m | 43 | 40d 7h 28m 15s | 6d 3h 32m 23s |
| Empty Interval | ||||
| 50d 1h 35m | 50d 14h 40m | 8 | 50d 8h 33m 45s | 17d 19h 17m 39s |
| 60d 7h | 60d 7h | 1 | 60d 7h | 60d 7h |
| 70d 5h 15m | 70d 5h 15m | 1 | 70d 5h 15m | 70d 5h 15m |
| From | To | Samples | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 55m | 22h 50m | 256 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |||||
| 10d 50m | 11d 2h 25m | 330 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |
| 20d 40m | 20d 21h 55m | 216 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | ||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 30d 35m | 30d 22h 40m | 111 | XX | XX | XX | XX | XX | XX | ||||||||||||||
| 40d 1h | 41d 2h 10m | 43 | XX | XX | ||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 50d 1h 35m | 50d 14h 40m | 8 | ||||||||||||||||||||
| 60d 7h | 60d 7h | 1 | ||||||||||||||||||||
| 70d 5h 15m | 70d 5h 15m | 1 |
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 8h 20m | 21d 4h 10m | 34 | 3d 15h 34m | 1d 1h 35m 34s |
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 8h 20m | 1d 11h 45m | 26 | 1d 23m 41s | 5h 5m 12s |
| Empty Interval | ||||
| Empty Interval | ||||
| Empty Interval | ||||
| 10d 9h 25m | 10d 14h 20m | 3 | 10d 12h 35m | 6d 1h 50m 5s |
| 11d 2h 30m 6s | 11d 7h 15m | 4 | 11d 5h 16m 16s | 5d 14h 38m 20s |
| Empty Interval | ||||
| Empty Interval | ||||
| Empty Interval | ||||
| 21d 4h 10m | 21d 4h 10m | 1 | 21d 4h 10m | 21d 4h 10m |
| From | To | Samples | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8h 20m | 1d 11h 45m | 26 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 10d 9h 25m | 10d 14h 20m | 3 | XX | |||||||||||||||||||
| 11d 2h 30m 6s | 11d 7h 15m | 4 | XX | XX | ||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 21d 4h 10m | 21d 4h 10m | 1 |
This shows the same phenomena as in the earlier simulation runs wherein the dramatic difference between times associated with different attack methods produces a set of time frames with few if any intervening cases. In this result we also see both the cases where the attacker wins and where the defender wins. The effect of a successful defense on any individual run is to defeat the attacker, and in this example, the presence of a weak defender has almost no effect on the results. If we compare the results in Table 6 with those in Table 9, we also see that the shortest time to attacker success is nearly the same (1h vs 55m), the maximum time to attacker success is about the same (70d 10h 55m vs. 70d 5h 15m), the mean time to attacker success is very close (13d 17h 31m 54s vs. 13d 23h 38m 48s) and the deviation of time till attacker success is nearly identical (13h 39m 41s 1h vs. 14h 9m 56s). But if we provide a much stronger defender, things begin to change substantially.
In Table 10 we show the same simulation parameters
except that the defender strength is increased from 20 percent to 90
percent. Because the defender does so well in this circumstance, we
have used 5,000 simulation runs to get more meaningful statistics.
(simset '(34) "Internet" "Frank" 90 5000) Run time: 1242.26 sec.
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 6h 5m | 91d 10h 25m | 77 | 14d 14h 16m 14s | 2d 16h 54m 12s |
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 6h 5m | 1d 6h 35m | 36 | 17h 56m 6s | 3h 12m 25s |
| 10d 6h 30m | 11d 12h | 14 | 10d 17h 31m 4s | 2d 20h 51m 15s |
| 20d 7h | 21d 18h 30m | 10 | 20d 22h 28m | 6d 14h 56m 16s |
| 30d 14h 25m | 31d 20h 10m | 10 | 30d 23h 11m | 9d 19h 1m 54s |
| 41d 4h 10m | 41d 4h 10m | 1 | 41d 4h 10m | 41d 4h 10m |
| 50d 15h 50m | 50d 23h 25m | 2 | 50d 19h 37m 30s | 35d 22h 24m 33s |
| 60d 22h 20m | 61d 16h 20m | 2 | 61d 7h 20m | 43d 8h 24m 33s |
| 70d 18h 55m | 70d 18h 55m | 1 | 70d 18h 55m | 70d 18h 55m |
| Empty Interval | ||||
| 91d 10h 25m | 91d 10h 25m | 1 | 91d 10h 25m | 91d 10h 25m |
| From | To | Samples | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6h 5m | 1d 6h 35m | 36 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | ||
| 10d 6h 30m | 11d 12h | 14 | XX | XX | XX | XX | XX | XX | XX | |||||||||||||
| 20d 7h | 21d 18h 30m | 10 | XX | XX | XX | XX | XX | |||||||||||||||
| 30d 14h 25m | 31d 20h 10m | 10 | XX | XX | XX | XX | XX | |||||||||||||||
| 41d 4h 10m | 41d 4h 10m | 1 | ||||||||||||||||||||
| 50d 15h 50m | 50d 23h 25m | 2 | XX | |||||||||||||||||||
| 60d 22h 20m | 61d 16h 20m | 2 | XX | |||||||||||||||||||
| 70d 18h 55m | 70d 18h 55m | 1 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 91d 10h 25m | 91d 10h 25m | 1 |
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 8h 25m | 81d 11h 10m 6s | 4923 | 8d 20h 44m 52s | 4h 36m 6s |
| From | To | Samples | Mean | St. Dev. |
|---|---|---|---|---|
| 8h 25m | 2d 11h 45m | 2533 | 1d 4h 23m 34s | 34m 26s |
| 10d 9h 5m | 12d 4h 10m | 1473 | 11d 5h 31m 40s | 7h 1m 27s |
| 20d 8h 20m | 22d 9h 20m | 613 | 21d 6h 53m 12s | 20h 38m 9s |
| 30d 12h 5m | 32d 11h | 203 | 31d 8h 42m 29s | 2d 4h 49m 56s |
| 40d 10h 10m | 40d 13h 35m | 2 | 40d 11h 52m 30s | 28d 15h 13m 13s |
| 40d 22h 50m | 42d 5h 15m 5s | 66 | 41d 10h 10m 17s | 5d 2h 22m 33s |
| 50d 9h 45m | 52d 6h 5s | 18 | 51d 10h 10m 52s | 12d 2h 54m 31s |
| 60d 11h 30m | 62d 7h 40m 6s | 14 | 61d 16h 3m 35s | 16d 11h 34m 18s |
| Empty Interval | ||||
| 81d 11h 10m 6s | 81d 11h 10m 6s | 1 | 81d 11h 10m 6s | 81d 11h 10m 6s |
| From | To | Samples | 127 | 254 | 381 | 508 | 635 | 762 | 889 | 1016 | 1143 | 1270 | 1397 | 1524 | 1651 | 1778 | 1905 | 2032 | 2159 | 2286 | 2413 | 2540 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8h 25m | 2d11h 45m | 2533 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |
| 10d 9h 5m | 12d 4h 10m | 1473 | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | XX | |||||||||
| 20d 8h 20m | 22d 9h 20m | 613 | XX | XX | XX | XX | ||||||||||||||||
| 30d 12h 5m | 32d 11h | 203 | XX | |||||||||||||||||||
| 40d 10h 10m | 40d 13h 35m | 2 | ||||||||||||||||||||
| 40d 22h 50m | 42d 5h 15m 5s | 66 | ||||||||||||||||||||
| 50d 9h 45m | 52d 6h 5s | 18 | ||||||||||||||||||||
| 60d 11h 30m | 62d 7h 40m 6s | 14 | ||||||||||||||||||||
| Empty | Interval | 0 | ||||||||||||||||||||
| 81d 11h 10m 6s | 81d 11h 10m 6s | 1 |
A couple of things come quickly to the fore. For successful attacks, the mean time to success is essentially unchanged from Table 9 to Table 10 (13d 23h 38m 48s vs. 14d 14h 16m 14s). The shortest time to successful attack has gone up substantially (55m vs. 6h 5m) but this may reflect only the total number of successful attacks (966 vs. 77) and perhaps with 50,000 runs we would end up with an attack that took only 55m. The maximum time to successful attack went up by a substantial amount (70d 5h 15m vs. 91d 10h 25m) which would seem to indicate that slower attacks work better. Even more impressive is the spreading of the standard deviation by more than a factor of four (14h 9m 56s vs. 2d 16h 54m 12s). This would seem to show that the uncertainty for the attacker has increased substantially, even for successful attacks.
One conclusion we can clearly see is that stronger defenders do a disproportionately better job of defeating attackers. This defender was only 8 times as good as the one in the previous example, and yet success rates went from 5 percent to 98 percent. At defensive strength 100, only one of a thousand attacks succeeded and it took about 11 days of effort. The mean time to defeat attacks was just a bit over 9 days 8 hours with an 11 hour standard deviation.
While doing a few thousand simulations takes a relatively small amount of computer time, one of the limiting factors in the use of simulation for real systems is the large size of the simulation space, and for making design decisions, the far larger size of the design space. To get a sense of this, consider that we can vary the strength of the attacker, the attacker type, the network architecture, the set of defenses in place at each point in the network, and that in order to get a realistic assessment of a rage of situations, we need to vary the from and to nodes as well.
To get a reasonable characterization of a simple system requires something like 10 different defender strengths and 15 different types of attackers. At 145 seconds per thousands simulations (see the timing information in Table 9), this comes to just over 6 hours and gives a plot that indicates how defender strength impacts probability of success and mean time to penetration across a range of threats.
To make a design decision about which combination of defenses would be best against a set of threats for a given network configuration would require that we look at all combinations of more than 90 defenses - 2^90 6 hour runs. This is clearly not a feasible way to do such an analysis.
Another important set of parameters relate to the question of how we allocate prevention, detection, and reaction resources. For example, is there a great benefit in decreasing reaction time for certain defenses or for the organization as a whole? Even a simplistic variation of this parameter would require a factor of 10 - or 60 hours - to evaluate a single design.
Fortunately, the simulation technique we apply here is inherently parallelizable and just about ideally scalable. We can simply allocate problems to processors in proportion to their processing speed to get near perfect parallelism. For example, with 20 computers available in a computer network we should be able to do the variation of defense strength parameters for all 36 classes of attackers by simply sending each computer a list of simulations to perform. Because this form of simulation is compute bound, communication between processors is only for the purpose of specifying simulations and getting back results. A typical network of personal computers with a standard communications network is perfectly adequate to the task.
In an experimental network configured for this purpose, we assigned the same port on each computer to run the simulation engine and sent simulations to be performed to each processor, taking results back as simulations were completed. The programming effort took about 15 minutes for a rough distribution system for this task and the process was reasonably effective at distributing the computation and returning results. In 140 minutes of real time, 20 400MHz PC processors running Linux performed 1000 simulations each for 35 threat profiles and 10 values of defender strength, or 350,000 simulation runs. This comes to 140 minutes for 350,000 simulations on 20 processors, or about 24 seconds per 1,000 simulation runs. This is not very good parallelism, since it comes to 480 seconds per 1000 runs per processor or about 3.4 times slower than the single processor runs done earlier. We have not spent any time to determine why the performance was so slow, but it is likely related to the shared file system used for communication between processors in this particular network and the manner in which we did program distribution. If this technique is to be used more extensively, performance bottlenecks will be worth removing.
Using the same problem set discussed above, we came
up with the results in Table 11 - summarized into defender wins out of
1000 runs - with colors ranging from red (better for the attacker) to
green (better for the defender). The results have been sorted (roughly)
from best for the attacker to worst for the attacker.
| Threat | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% |
|---|---|---|---|---|---|---|---|---|---|---|
| infrastructure-warriors | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vandals | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 48 | 222 | 691 |
| hoodlums | 0 | 1 | 7 | 30 | 85 | 232 | 463 | 665 | 916 | 1000 |
| government-agencies | 0 | 4 | 18 | 50 | 86 | 153 | 275 | 439 | 623 | 858 |
| crackers-for-hire | 0 | 5 | 9 | 24 | 60 | 111 | 245 | 399 | 600 | 871 |
| consultants | 0 | 8 | 17 | 40 | 102 | 196 | 336 | 500 | 682 | 914 |
| vendors | 1 | 1 | 8 | 21 | 55 | 103 | 193 | 289 | 538 | 744 |
| information-warriors | 1 | 4 | 19 | 28 | 94 | 162 | 246 | 419 | 600 | 864 |
| tiger-teams | 1 | 4 | 11 | 52 | 104 | 156 | 289 | 436 | 643 | 870 |
| military-organizations | 1 | 7 | 24 | 38 | 110 | 173 | 338 | 485 | 704 | 906 |
| cyber-gangs | 1 | 8 | 33 | 76 | 189 | 303 | 552 | 752 | 912 | 984 |
| whistle-blowers | 1 | 8 | 29 | 53 | 124 | 276 | 440 | 660 | 827 | 963 |
| foreign-agents-and-spies | 1 | 9 | 25 | 47 | 94 | 181 | 293 | 460 | 675 | 864 |
| insiders | 1 | 10 | 35 | 88 | 167 | 256 | 438 | 597 | 794 | 939 |
| industrial-espionage-experts | 1 | 10 | 24 | 43 | 105 | 172 | 304 | 376 | 598 | 840 |
| economic-rivals | 1 | 14 | 34 | 86 | 165 | 311 | 510 | 692 | 848 | 968 |
| nation-states | 2 | 7 | 27 | 63 | 145 | 232 | 369 | 512 | 722 | 916 |
| professional-thieves | 2 | 12 | 39 | 81 | 192 | 346 | 504 | 693 | 868 | 981 |
| drug-cartels | 3 | 12 | 54 | 89 | 190 | 309 | 457 | 632 | 774 | 942 |
| maintenance-people | 3 | 21 | 71 | 148 | 302 | 508 | 685 | 849 | 952 | 989 |
| extortionists | 4 | 17 | 63 | 103 | 253 | 402 | 619 | 761 | 908 | 983 |
| customers | 4 | 41 | 104 | 205 | 359 | 554 | 755 | 913 | 950 | 993 |
| global-coalition | 5 | 6 | 36 | 51 | 102 | 190 | 370 | 521 | 708 | 917 |
| activists | 5 | 24 | 77 | 163 | 309 | 501 | 666 | 838 | 930 | 974 |
| police | 5 | 36 | 87 | 242 | 367 | 574 | 744 | 880 | 962 | 993 |
| crackers | 5 | 50 | 135 | 317 | 478 | 710 | 860 | 951 | 983 | 999 |
| competitors | 7 | 62 | 182 | 351 | 548 | 775 | 900 | 968 | 992 | 1000 |
| paramilitary-groups | 9 | 35 | 126 | 251 | 441 | 685 | 823 | 938 | 990 | 1000 |
| deranged-people | 12 | 54 | 164 | 333 | 544 | 745 | 912 | 973 | 995 | 998 |
| terrorists | 13 | 66 | 163 | 356 | 534 | 769 | 880 | 980 | 987 | 997 |
| organized-crime | 14 | 53 | 162 | 281 | 478 | 702 | 852 | 946 | 986 | 999 |
| private-investigators | 14 | 66 | 181 | 404 | 641 | 840 | 954 | 990 | 998 | 1000 |
| reporters | 18 | 87 | 197 | 411 | 657 | 821 | 949 | 985 | 998 | 1000 |
| club-initiates | 22 | 102 | 267 | 490 | 740 | 893 | 964 | 992 | 997 | 1000 |
| hackers | 23 | 75 | 159 | 345 | 544 | 776 | 931 | 976 | 991 | 999 |
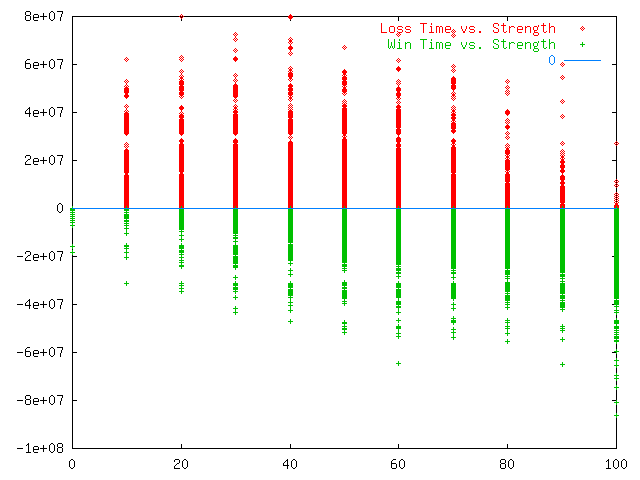
The scatter plot in plate 2 shows the underlying data across all threats with the X-axis indicating defender strength and the Y-axis indicating time. The red indicates cases where attacks succeed and the green indicates cases where the defense defeats the attack. Successful defenses are plotted as negative times so that they can be seen in juxtaposition to the successful attacks. Note that earlier success for an attacker or defender is beneficial, so that points closer to the 0 line are better for either attacker or defender, while a larger volume indicates more wins. This plot clearly shows the clustering described earlier with dead bands where no color appears showing periods of time in which no action took place.
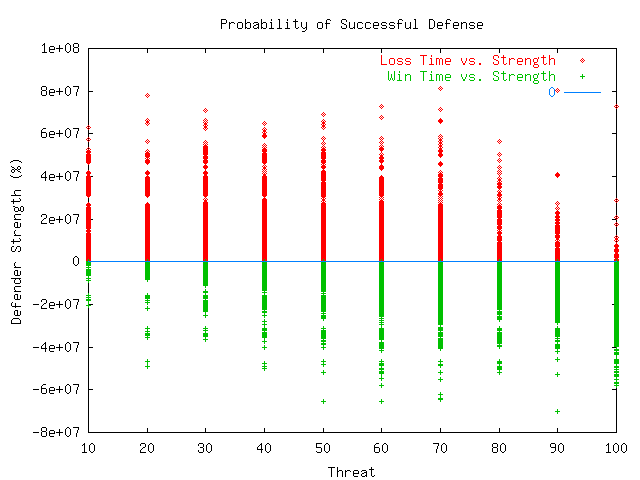
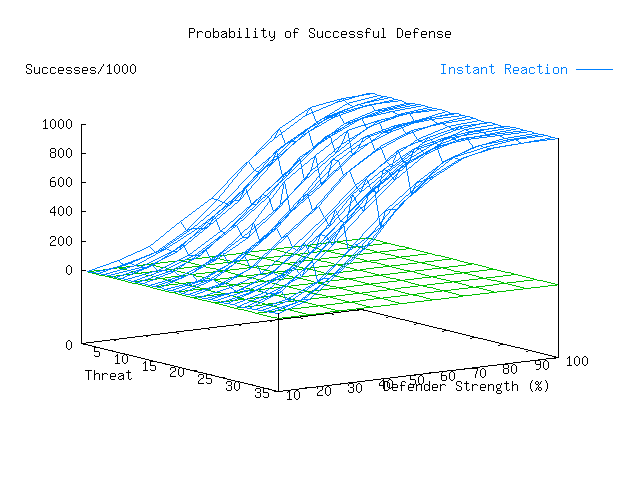
Plate 3 shows the contour of the probability of successful defense, and makes it clear that there is a nonlinearity of success with defender strength. It displays different threat types along the X axis, the defender strength along the Y-axis, and the the number of successful defenses per 1000 attacks along the Z-axis. A zero grid is also shown (in green) for perspective.
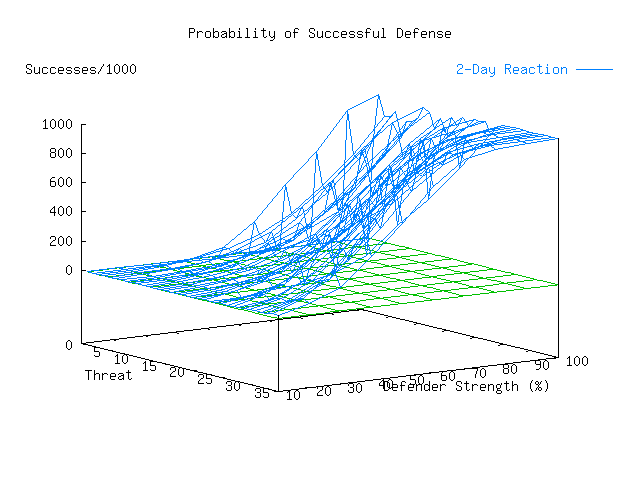
This summary information is enlightening in several ways. Perhaps the most interesting is the result indicating that even with a perfect defender, certain threat profiles are never defeated. At first glance, this might seem to indicate that the defender simply had mismatched defenses for the attack mechanisms used by the threat. This notion turns out to be wrong. In fact, the poor performance in this case relates to the effects of detection and response time on the ability to defeat an attacker. The infrastructure warrior threat profile assumes that the attacker only uses techniques that are very fast and that the attacker is highly skilled. Even though large portions of attempted attacks tend to be detected, the defending organization cannot react in time to prevent the harm. As we vary the organization's detection and response time, the overall picture changes dramatically.
Another similar run, shown in Table 12, Plate 4, and
Plate 5, was done with detection and response times of 1 second each and
all other parameters identical. The reaults in Table 12 are again sorted
most successful for the attacker to least successful for the attacker.
| Threat | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% |
|---|---|---|---|---|---|---|---|---|---|---|
| Information Warriors | 4 | 51 | 118 | 264 | 400 | 599 | 757 | 890 | 953 | 991 |
| Hoodlums | 7 | 25 | 90 | 212 | 404 | 632 | 838 | 952 | 992 | 1000 |
| Whistle Blowers | 7 | 54 | 112 | 235 | 393 | 581 | 735 | 863 | 964 | 993 |
| Government Agencies | 8 | 42 | 137 | 247 | 383 | 582 | 762 | 894 | 955 | 994 |
| Industrial Espionage Experts | 9 | 42 | 125 | 253 | 425 | 625 | 777 | 911 | 977 | 997 |
| Global Coalitions | 9 | 53 | 134 | 279 | 431 | 651 | 823 | 923 | 972 | 996 |
| Maintenance People | 9 | 72 | 193 | 365 | 528 | 755 | 882 | 960 | 995 | 999 |
| Vendors | 10 | 49 | 128 | 263 | 425 | 590 | 761 | 897 | 963 | 984 |
| Military Organizations | 11 | 55 | 132 | 264 | 434 | 607 | 799 | 919 | 974 | 994 |
| Customers | 11 | 62 | 142 | 319 | 508 | 683 | 847 | 940 | 985 | 996 |
| Extortionists | 11 | 70 | 192 | 332 | 506 | 744 | 863 | 966 | 988 | 999 |
| Foreign Agents and Spies | 12 | 42 | 128 | 263 | 413 | 597 | 758 | 904 | 972 | 997 |
| Nation States | 12 | 56 | 147 | 267 | 453 | 667 | 828 | 934 | 985 | 996 |
| Competitors | 12 | 83 | 207 | 380 | 635 | 791 | 933 | 978 | 998 | 999 |
| Tiger Teams | 13 | 42 | 128 | 266 | 435 | 596 | 770 | 903 | 957 | 995 |
| Activists | 13 | 53 | 163 | 293 | 490 | 658 | 827 | 917 | 968 | 992 |
| Deranged People | 13 | 66 | 179 | 356 | 556 | 791 | 917 | 971 | 995 | 1000 |
| Police | 13 | 83 | 212 | 378 | 590 | 796 | 932 | 979 | 996 | 1000 |
| Organized Crime | 14 | 57 | 139 | 318 | 485 | 699 | 838 | 930 | 980 | 998 |
| Insiders | 14 | 75 | 176 | 350 | 523 | 744 | 882 | 965 | 985 | 997 |
| Crackers for Hire | 15 | 57 | 126 | 275 | 457 | 647 | 790 | 914 | 974 | 995 |
| Consultants | 16 | 39 | 120 | 260 | 407 | 610 | 755 | 899 | 957 | 991 |
| Professional Thieves | 16 | 57 | 152 | 333 | 529 | 714 | 884 | 948 | 994 | 998 |
| Drug Cartels | 16 | 63 | 129 | 265 | 454 | 643 | 813 | 914 | 983 | 995 |
| Infrastructure Warriors | 16 | 67 | 151 | 301 | 462 | 637 | 815 | 917 | 976 | 988 |
| Hackers | 16 | 85 | 201 | 414 | 661 | 807 | 925 | 976 | 998 | 1000 |
| Vandals | 17 | 78 | 212 | 407 | 611 | 802 | 933 | 981 | 994 | 1000 |
| Crackers | 17 | 80 | 173 | 354 | 565 | 750 | 900 | 975 | 990 | 1000 |
| Reporters | 17 | 88 | 240 | 447 | 688 | 842 | 949 | 992 | 1000 | 1000 |
| Club Initiates | 20 | 109 | 298 | 529 | 740 | 884 | 978 | 1000 | 1000 | 1000 |
| Economic Rivals | 23 | 69 | 166 | 341 | 483 | 684 | 878 | 953 | 986 | 997 |
| Paramilitary Groups | 26 | 73 | 197 | 410 | 609 | 774 | 905 | 976 | 994 | 998 |
| Cyber Gangs | 27 | 66 | 206 | 389 | 621 | 789 | 928 | 971 | 1000 | 1000 |
| Terrorists | 30 | 98 | 237 | 405 | 633 | 817 | 924 | 975 | 985 | 999 |
| Private Investigators | 32 | 103 | 271 | 445 | 693 | 837 | 945 | 991 | 997 | 1000 |
Because detection and response were faster, far more of the attacks were mitigated far sooner. This dramatically changes the ordering of which attackers are most successful. For example, infrastructure warriors, who were undefeatable with slow detection and response, move to one of the less effective threats, while information warriors move up 6 places to become the most dangerous threat. The more rapid defense also reduces simulation time considerably, indicating that the total number of events that took place were dramatically reduced. This entire run of 350,000 simulations took only about 40 minutes of real-time on the same computer network used for the previous parallel run, or about a factor of 4 reduction in total moves. The reduction in moves corresponds roughly to a reduction in effort, and the implication would seem to be that faster response means less response and reduced cost. This has not been studied in further depth in this effort, but it is clearly worth looking into.
Another interesting result of these runs is the shape of the curves for each threat as a function of defensive strength. It is clearly non-linear. This would seem to indicate that the return on investment in the quality of a defender is non-linear. In other words, with faster detection and reaction, the skill of the defender becomes less critical to success. Plate 6 contrasts the two cases just discussed and a third case discussed below. It plots all three surfaces from a 'side' view that contrasts the shape of the response functions. The colors labeled 2-Day Reaction, One Level, and Instant correspond respectively to the 2-day reaction time example from Plate 3, an example which uses instant reaction but removes defense-in-depth, and the instant reaction with defense-in-depth from Plate 5.. The red surface is the zero plane.
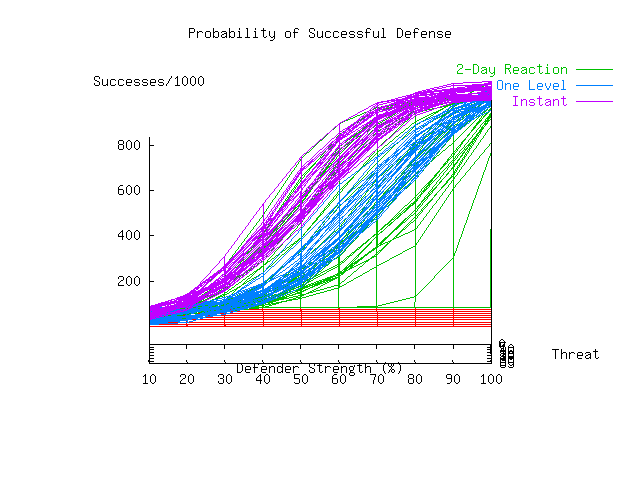
One speculative reason for the non-linearity of the curves is that the attacker must go through several defenses in sequence. Even if each defense is linear in the defender strength, the probabilities for a sequence of linear phenomena add up to a non-linear result because any successful defense causes the attack graph to be severed, and no progress is made toward later defenses. Plate 6 shows the same situation with attacks only going from the Internet to Angel. This requires only one successful attack for success, and it is noteworthy that the resulting set of surfaces are closer to linear than either of the other two. This simulation would seem support this theory, but it is hardly definitive.
As an aside, the fact that the overall curve has moved to the right in this simulation where a firewall alone was used, (one-level) as compared to the simulation in which defense-in-depth was used (instant-reaction), might give the notion that defense-in-depth has real value in terms of reducing the requirement for expertise in operational aspects of protection. To get at this more clearly, we need to place the same defenses in each situation. Also note that the one-level defense is better in many cases than the full set of defenses with two-day reaction times. Thus it appears that we may be more successful by being faster in our detection and reaction than by having more defenses that are slower. The precise tradeoff point that optimizes the set and placement of defenses and reaction times for any given situation is too complex to determine for any realistic circumstance, but finite sets of prevention and reaction schemes can clearly be compared and contrasted through this technique.
In Plates 7, 8, and 9, we examine the effects of time in more detail by displaying the strength vs. defender-wins curve for different times ranging from instant to 80 hours (3.33 days). It is noteworthy that the threat dictates the requirement for reaction speed. This is however somewhat simplistic because, as we will see later, it ignores the issue of strategies.
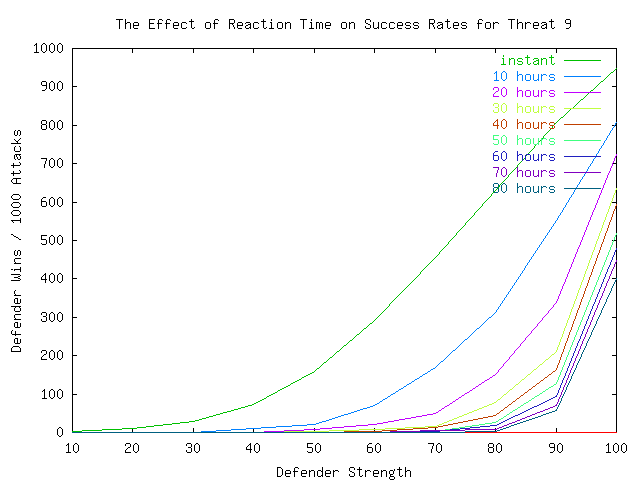
Whistle blowers do things on time scales of hours to days, so a result, the detection and reaction times are about exponential in the range being shown in Plate 7. Revisiting the earlier results from Tables 5, 6, 9, and 10, whose results indicate the time till successful attack, we see that, while they are discontinuous, on the large scale the number of attacks taking longer times go down approximately exponentially with time. Thus the exponential decrease in effectiveness as a function of reaction time seems natural.
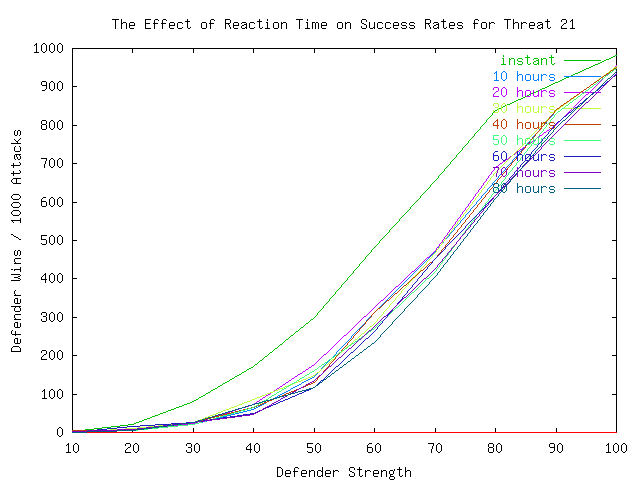
Deranged people, as shown in Plate 8, typically do something crazy every once in a while, so reaction time is not all that important. The types of attacks they tend to use are not extremely fast and they are relatively easy to defend against. Thus the difference between a three day reaction time and instantaneous reaction is only about 15 percent at its maximum.
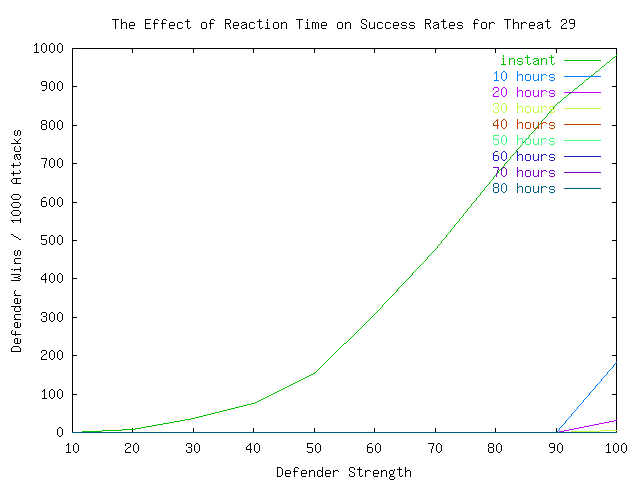
Infrastructure warriors are typically very fast and very harsh. As a result, in Plate 9 we see that rapid reaction is critical to success. In this example, we see that the first 10 hours of delay are very costly, consuming 80 percent of the cases. At 20 hours, we are up to more than 95 percent defeats for the defender, and if we wait 30 hours, the defender almost never wins. For this threat in the situation analyzed, rapid reaction is critical to success. If we want to know how rapid, we must examine the area of the curve between instant reaction and 10 hours in more detail.
A very interesting result that combines these results with the previous results on the distribution of successful attack times, is that the effect of faster reaction time on outcomes is highly non-linear. In fact, effectiveness of defense is not even monotonically improved by decreased reaction time. This is because of the bands of time in which there are no successful attacks. If reaction time is at the end of a one of these dead bands, moving it to the other end of the dead band has no effect on the success rates of defenders. Since faster reaction generally costs more, being at the high-speed end of a dead band is typically less cost effective than being at the low-speed end of the same dead band. In fact, since decisions taken over longer times have a tendency to be better thought out, there may be advantages in terms of the quality of the outcomes to taking the extra time to make a decision when time is available. For example, in Table 9 (1000 runs of a paramilitary group attacking Frank from the Internet with defender strength at 20%) there is a large dead band between 21 and 30 days in which speed is of no import.
This discussion has also neglected the notion that defense in depth itself is indicative of a stronger defender, and would seem to lend credence to the notion that having more expertise in the design of a defense makes the quality of the day-to-day defenders less important. Faster detection and response tends to move the curves to the left - in favor of poorer quality defenders, but remember that poorer quality defenders tend to be less responsive and achieving this result may be infeasible.
This brings up yet another limitation of simulation. While we may be able to simulate nearly instantaneous response, we are unlikely to be able to achieve it in many cases.
While these results help to show the power of parallel simulation in this application, this is only the tip of the proverbial iceberg. The full results of these simulations can be used to generate and analyze a wide range of other data such as the clustering phenomena shown in Plate 2 and how clustering is affected by defender strength and strategies, the time spectrum associated with attacks and defenses, and so forth.
While theoretically, you can get the same results sequentially as you can with parallelism, in practice, the time taken in simulation can be a real impediment to progress, and the inability to perform rapid experiments and examine the underlying data inhibits the generation and testing of ideas. Parallelism brings the scientific method closer to real-time, and even the small performance improvements shown in our examples can be quite a substantial advantage.
Prevention, detection, reaction, and consequences of attacks, all have costs associated with them, and to here, we have ignored costs as an issue. Costs are easily added to a simulation of this sort by assessing a fixed and per use cost of each attack and defense method and summing the costs from each simulation run. Since fixed costs are based on the defenses placed or attack capabilities available, regardless of the specific simulation run, the simulation need only assess per use costs.
Similarly, we can evaluate costs of consequences by assessing figures to worst case consequence, but this does not fully address the issue from a risk management perspective because all losses are not maximum valued, and no current or anticipated theory addresses the time effect of unmitigated attacks on consequences. As far as anybody seems to be able to tell today, consequences are highly dependent on a wide range of factors including but not limited to, the specifics of the information environment, the interdependencies within the organization, the ability of the systems and people to adapt to adverse circumstances, market conditions, public perceptions, the broader business environment, and on and on. To make matters even worse, in many real-world situations, the costs of consequences vary over several orders of magnitude depending on who you ask about them. The computer virus that spread through the Internet in 1988 [Rochlis89] is a good example in which after-the-fact estimates of loss ranged from hundreds of thousands of dollars to hundreds of millions of dollars.
It is our belief that consequence modeling of the sort required for this sort of analysis is beyond the scope currently attainable by simulation technologies. For that reason, we take the view that consequences are independent of the method by which an attacker gains access to an information system, and revert to a model in which the expert analyst assesses the situation and creates a distribution function that characterizes how much harm can be done in how much time by what sort of an attacker once the target has been defeated. We call this the characteristic loss function. Consequences fall out of the final results of the sorts of simulations shown herein. The result is generated by evaluating the characteristic loss function for each threat with a probability given by the simulation results. The probability is derived through simulation based on the strength of the defenders. The loss per unit time is derived by factoring in a rate of attempted attacks by each threat profile based on empirical data.
For the purposes of this example, we will take the results from the simulation runs with instantaneous reaction and assume that the frequency of attack and consequences from threats are taken from Table 13. This table does not reflect an actual organization but that each value used probably applies to some organization. We are also using a constant value for expected loss. A probability distribution is probably more useful in a real situation. Clearly this represents a large multinational organization of some sort.
| Threat | Mean Time To Attack | Expected Loss |
|---|---|---|
| Information Warriors | 10 years | 100,000,000 |
| Hoodlums | 6 months | 100,000 |
| Whistle Blowers | 3 years | 1,000,000 |
| Government Agencies | 3 years | 100,000 |
| Industrial Espionage Experts | 1 months | 10,000,000 |
| Global Coalitions | 6 months | 10,000,000 |
| Maintenance People | 2 months | 100,000 |
| Vendors | 1 months | 100,000 |
| Military Organizations | 10 years | 10,000,000 |
| Customers | 1 months | 100,000 |
| Extortionists | 1 years | 10,000 |
| Foreign Agents and Spies | 6 months | 10,000,000 |
| Nation States | 10 years | 100,000,000 |
| Competitors | 3 months | 10,000,000 |
| Tiger Teams | 3 years | 1,000,000 |
| Activists | 1 years | 10,000,000 |
| Deranged People | 2 years | 10,000 |
| Police | 2 months | 100,000 |
| Organized Crime | 2 months | 1,000,000 |
| Insiders | 2 weeks | 10,000,000 |
| Crackers for Hire | 3 months | 10,000,000 |
| Consultants | 3 months | 1,000,000 |
| Professional Thieves | 1 years | 1,000,000 |
| Drug Cartels | 20 years | 100,000 |
| Infrastructure Warriors | 10 years | 10,000,000 |
| Hackers | 1 days | 2,000 |
| Vandals | 1 months | 5,000 |
| Crackers | 1 hours | 10,000 |
| Reporters | 3 months | 5,000 |
| Club Initiates | 3 months | 5,000 |
| Economic Rivals | 1 months | 10,000,000 |
| Paramilitary Groups | 3 years | 10,000,000 |
| Cyber Gangs | 4 years | 1,000,000 |
| Terrorists | 6 months | 1,000,000 |
| Private Investigators | 2 months | 10,000 |
We can now compute an annual expected loss chart by
multiplying the probability of successful attack by attack frequency and
expected loss. The calculation is straight forward. For example, for
Information Warriors with the defender at 90 percent strength, 953 of
1000 attacks fail. If the Mean Time to Attack (MTTA) is 10 years and
4.7 percent of the time they succeed, there is a 0.47 percent chance of
a 100,000,000 dollar loss in any given year, or an expected loss of
470,000 per year. If we went to 100 percent defender strength this
would change to a 90,000 dollar expected loss per year, or a 380,000
dollar change in expected loss. If we sum up the expected loss for each
strength level across all threats, we get the total expected loss per
year as a function of defender strength, and we can then make a prudent
decision based on the tradeoff between quality and cost of defenders.
The results are shown in Table 14:
| Threat | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% |
|---|---|---|---|---|---|---|---|---|---|---|
| Information-Warriors | 9960000 | 9490000 | 8820000 | 7360000 | 6000000 | 4010000 | 2430000 | 1100000 | 470000 | 90000 |
| Hoodlums | 201358 | 197708 | 184527 | 159788 | 120855 | 74622 | 32850 | 9733 | 1622 | 0 |
| Whistle-Blowers | 331000 | 315333 | 296000 | 255000 | 202333 | 139666 | 88333 | 45666 | 12000 | 2333 |
| Government-Agencies | 33066 | 31933 | 28766 | 25100 | 20566 | 13933 | 7933 | 3533 | 1500 | 200 |
| Industrial-Espionage-Experts | 120571666 | 116556666 | 106458333 | 90885000 | 69958333 | 45625000 | 27131666 | 10828333 | 2798333 | 365000 |
| Global-Coalitions | 20095277 | 19203055 | 17560555 | 14620277 | 11538055 | 7076944 | 3589166 | 1561388 | 567777 | 81111 |
| Maintenance-People | 602858 | 564533 | 490925 | 386291 | 287133 | 149041 | 71783 | 24333 | 3041 | 608 |
| Vendors | 1204500 | 1157050 | 1060933 | 896683 | 699583 | 498833 | 290783 | 125316 | 45016 | 19466 |
| Military-Organizations | 989000 | 945000 | 868000 | 736000 | 566000 | 393000 | 201000 | 81000 | 26000 | 6000 |
| Customers | 1203283 | 1141233 | 1043900 | 828550 | 598600 | 385683 | 186150 | 73000 | 18250 | 4866 |
| Extortionists | 9890 | 9300 | 8080 | 6680 | 4940 | 2560 | 1370 | 340 | 120 | 10 |
| Foreign-Agents-and-Spies | 20034444 | 19426111 | 17682222 | 14944722 | 11903055 | 8171944 | 4907222 | 1946666 | 567777 | 60833 |
| Nation-States | 9880000 | 9440000 | 8530000 | 7330000 | 5470000 | 3330000 | 1720000 | 660000 | 150000 | 40000 |
| Competitors | 40068888 | 37189444 | 32160555 | 25144444 | 14802777 | 8476111 | 2717222 | 892222 | 81111 | 40555 |
| Tiger-Teams | 329000 | 319333 | 290666 | 244666 | 188333 | 134666 | 76666 | 32333 | 14333 | 1666 |
| Activists | 9870000 | 9470000 | 8370000 | 7070000 | 5100000 | 3420000 | 1730000 | 830000 | 320000 | 80000 |
| Deranged-People | 4935 | 4670 | 4105 | 3220 | 2220 | 1045 | 415 | 145 | 25 | 0 |
| Police | 600425 | 557841 | 479366 | 378383 | 249416 | 124100 | 41366 | 12775 | 2433 | 0 |
| Organized-Crime | 5998166 | 5736583 | 5237750 | 4148833 | 3132916 | 1831083 | 985500 | 425833 | 121666 | 12166 |
| Insiders | 257064285 | 241160714 | 214828571 | 169464285 | 124360714 | 66742857 | 30764285 | 9125000 | 3910714 | 782142 |
| Crackers-for-Hire | 39947222 | 38243888 | 35445555 | 29402777 | 22021666 | 14316111 | 8516666 | 3487777 | 1054444 | 202777 |
| Consultants | 3990666 | 3897388 | 3568888 | 3001111 | 2404944 | 1581666 | 993611 | 409611 | 174388 | 36500 |
| Professional-Thieves | 984000 | 943000 | 848000 | 667000 | 471000 | 286000 | 116000 | 52000 | 6000 | 2000 |
| Drug-Cartels | 4920 | 4685 | 4355 | 3675 | 2730 | 1785 | 935 | 430 | 85 | 25 |
| Infrastructure-Warriors | 984000 | 933000 | 849000 | 699000 | 538000 | 363000 | 185000 | 83000 | 24000 | 12000 |
| Hackers | 718320 | 667950 | 583270 | 427780 | 247470 | 140890 | 54750 | 17520 | 1460 | 0 |
| Vandals | 59799 | 56088 | 47936 | 36074 | 23664 | 12045 | 4075 | 1155 | 365 | 0 |
| Crackers | 86110800 | 80592000 | 72445200 | 56589600 | 38106000 | 21900000 | 8760000 | 2190000 | 876000 | 0 |
| Reporters | 19933 | 18493 | 15411 | 11213 | 6326 | 3203 | 1034 | 162 | 0 | 0 |
| Club-Initiates | 19872 | 18067 | 14235 | 9550 | 5272 | 2352 | 446 | 0 | 0 | 0 |
| Economic-Rivals | 118868333 | 113271666 | 101470000 | 80178333 | 62901666 | 38446666 | 14843333 | 5718333 | 1703333 | 365000 |
| Paramilitary-Groups | 3246666 | 3090000 | 2676666 | 1966666 | 1303333 | 753333 | 316666 | 80000 | 20000 | 6666 |
| Cyber-Gangs | 243250 | 233500 | 198500 | 152750 | 94750 | 52750 | 18000 | 7250 | 0 | 0 |
| Terrorists | 1966944 | 1829055 | 1547194 | 1206527 | 744194 | 371083 | 154111 | 50694 | 30416 | 2027 |
| Private-Investigators | 58886 | 54567 | 44347 | 33762 | 18675 | 9915 | 3345 | 547 | 182 | 0 |
| TOTALS | 756275652 | 716769854 | 644161811 | 519273740 | 384095519 | 228841887 | 110941682 | 39876095 | 13002391 | 2213951 |
These results are particularly interesting because the threats that are more important in terms of financial loss change with the defender's strength. At low defender quality, crackers are ranked 4th from the highest consequence, while at high defender strength, crackers are ranked last. On the other hand, insiders dominate throughout the process as the highest expected loss contributor, with their effect on the order of 1/3 of the total expected loss and becoming slightly more dominant as the defender becomes better able to fend of other attacks. The cause of insider dominance is not trivially assessed from these results, and this should not be taken without more detailed examination as indicating a root cause for insiders dominating actual harm in the real world.
As the defenders get to high levels of quality, the expected loss drops down to only about two million dollars per year. While this data is not accurate in the sense of being prescriptive, it is not unrealistic for large organizations. It is easy to believe that different protective schemes would vary in cost by this much and that, if the sensitivity to the quality of defense is as these results would seem to indicate, marginal improvements in protection effectiveness might have large enough financial impacts to warrant in-depth examination. Even at this relatively mildly sloped area of the curve, small improvements in defender quality are worth substantial efforts.
In addition, at this cost level, response costs may become quite important. This example has defenders fielding more than one attack per hour, or almost 9,000 attacks per year. Even if the average reaction only costs one hundred dollars - including the personnel, systems, and infrastructure that have to be there to handle it - this is half of the expected loss at 100% defender strength.
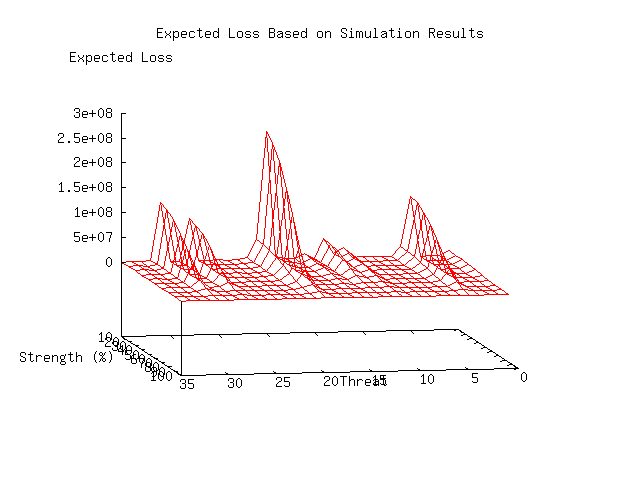
The dominance of individual threats (Plate 10) is also interesting, but it is important to not pay too much attention to this sort of effect when the data used for these examples is not specific to a particular organization and not validated for any particular use.
Perhaps more important and more enduring is the financial roll-up of expected loss plotted against defender strength as shown in Plate 11. In this case, the knee point for expected loss comes at about 80 percent of maximum defender strength, but again, the specifics of this case are almost certainly not relevant to the reader. What is relevant is the notion that from this data we can compute the cost of talent against the benefit in expected loss reduction and find the proper tradeoff point.
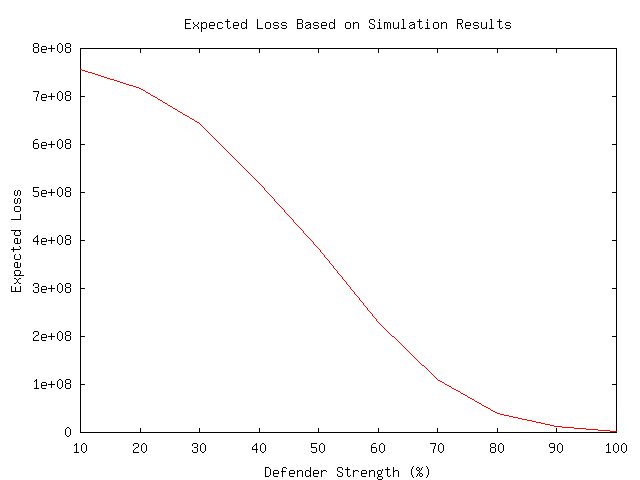
If we add in detailed defender costs, this picture changes rather interestingly. It turns out that the cost of increasing the quality of defenders goes up rather steeply as we approach perfection, while going from little expertise to fairly good expertise is far less expensive. With the right education, for ten to twenty thousand dollars per defender, we can go from a defender of strength 10% to a defender of strength 60% to 70%. For another twenty thousand dollars, we may be able to get to strength 80%, but getting to 100% is essentially impossible at any price. For the curve above, this would seem to indicate that we should spend about thirty thousand dollars per year to train security specialists (assuming they are systems administrators and have other expertise already). If we spend much more, it will likely not be worth the cost, while spending less is probably inadequate. Of course this depends heavily on the quality of the training you get for the cost and many other factors. Again, these results are not prescriptive for other cases, but they do seem to demonstrate that the technique is effective in that it is able to produce prescriptive results given reasonably accurate data.
Up until this point, we have assumed that attackers use random selection to pick attacks out of a set of available attack methods, but realistically, human attackers use non-random strategies to make their selections. For example, some take what they perceive to be the path of least resistance, while others take the path of least detection, and still others select attacks based on speed. The strategic decisions made by attackers substantially changes the manner in which simulations proceed.
In an ideal world, we would analyze all strategies and come up with optimal attacker and defender decisions, but we don't live in such a world, and the nature of the attack and defense situation precludes any fixed optimal strategy. From a game theoretic standpoint, our simulations study a two-person repeated non-zero-sum game with imperfect information. There are no equilibria, the number of possible strategies is the number of combinations of attack methods (about 2^95) for the attacker and the number of combinations of defense methods (about 2^150) for the defender at each node in the sequence from the source of the attack to its destination. Furthermore, this may be a game with uncommon objectives in that the attacker's efforts may not be directly opposed to the defender's efforts, and yet it is not a cooperative game in the sense that the parties do not exchange information in order to gain common objectives.
While we don't propose to analyze strategies in this paper, there are some clear strategic notions that arise out of our results - primarily the notions of stealth and speed for the attacker and speed and skill for the defender. The stealth strategy is one where the attacker tries to use methods that are unlikely to be detected, while the speed strategy exploits high speed attacks in the hopes that the likelihood of success before detection and reaction is higher. The defensive strategy of speed for the defender is addressed by the reaction time analysis above, as is the notion of defender strength.
Our results clearly show that there are advantages to speed for an attacker, but only to the extent that the defender takes time to detect and react. Based on these results, a strong attack strategy would seem to be to attack as quickly as possible for a period of time less than the response time of the defenders, while doing so in a manner that is hard to trace after the fact. When you reach the time to defend, stop, and try from somewhere else. There is also a clear advantage to knowing more about the defender's defenses because the more that attacker knows, the more likely that will be to find a workable stealth strategy. Similarly, intelligence can be used to determine reaction times. One way to do this is by testing the defenses and observing for reactions. For this reason, it might be prudent for defenders to not demonstrate their full reaction capability on every attack. Thus the deception strategy wherein attacks are rerouted to a honey pot may be more effective than simply defeating an attacker by forceful termination of sessions. Needless to say, this discussion could go one almost without end. The point to be made in this context, however, is that strategies can be analyzed using simulation and that analysis is revealing.
Clearly strategies are a substantive issue and, at least for now, they will be left for future efforts. Similar efforts in evaluating strategies have been used in a wide range of subject areas including military strategic analysis and in training exercises.
For the purposes of simulation, models are both driven and limited in their accuracy by a set of measurements that are used to determine the characteristic functions that set the values used in runs. If these values are ridiculous, the meaning of the simulation is clearly lost and it becomes nothing more than an academic exercise. The pressing questions then are; (1) How good do these values have to be in order to provide what level of quality in the results of the simulation? and (2) How do we get them to that level of quality?
The theory of measurement posits that there are four classes of measurements; (1) nominal, (2) ordinal, (3) interval, and (4) ratio.
Examples of (nearly) nominal measurements are the attack, defense, and threat categories used in our model. They would be nominal except that they are not mutually exclusive and may not be collectively exhaustive, although we try to make them so. The physical informational, and systemic as well as theoretical< demonstrated, and widespread measurements used in the model do meet the requirements of nominality.
We do not currently use ordinal measurements (strict ordering by relation) but we do use the closely related partial ordering in our descriptions of the flow of an attack from source to destination.
Intervals (ordinals with a constant distance and size for ranges) are used in our analysis of results and - to a limited extent as a side effect of limits on granularity. For example, the analysis above used 10%, 20%, ... 100% for defender strength.
We use integer-valued ratios, such as times and strength measures, which are characterized by their meaningful zero point and meaningful ratios between numbers.
We call the intervals and ratios that we use metrics because they are essentially treated as linear measurements. The question of how good these metrics have to be depends largely on two factors; (1) their intended use, and (2) the sensitivity of results to their quality. The question of how we attain the desired level of quality depends largely on the answers to the first question.
If the intended use were to, for example, predict specifically how a specific system would act under specific attack and defense conditions, the level of detail and accuracy required would be so extreme that we would likely never be able to attain it unless we designed a special purpose simulation for the specific case of interest. This demonstrates the contrast between the simulation of, for example, an electronic component, and the simulation of attacks and defenses on computer systems. Every bit of state in a computer system has the potential of dramatically changing the outcome of an attack, and these bits change so rapidly that we cannot even do a completely accurate snapshot backup of a typical computer while it is in operation. Clearly we cannot hope to simulate it at that level of accuracy in a timely enough fashion to be meaningful.
We are limited by what we can realistically hope to achieve, and yet for simulation to be meaningful, we need to be able to gain some predictive value from the effort. Again there seems to be an advantage in looking at two views; (1) the value of absolute results, and (2) the value of relative results. While it would be nice to achieve absolute results in our simulations, there may also be significant value in achieving only relative results. An example is demonstrated in the form of relativistic risk analysis.[Cohen9706] In this technique, we need not know absolute values to be able to compare different system configurations and get relative advantages and disadvantages. While relativistic analysis may not be definitive in terms of the numerical values of results, it can definitely provide results in terms of the advantage of one method over another. Simulation based on relative metrics requires only that the system of measurement be meaningful in a relative sense. The elimination of the requirement for absolute values has many advantages. We see this effect in this paper when, for example, we compare different reaction times and their effect on protection (i.e., Plates 6, 7, 8, and 9). Even if the absolute values of the results are completely wrong, the result appears to be valuable. To the extent that we can get accurate absolute results, this is, of course, all the more helpful, since such results can be used as a rational basis for making design and risk management decisions.
For now, let us then limit our fields of applicability to gaining a deeper understanding of the structure and nature of sequential attacks and defenses, the effects of different design and operational decisions, analysis of strategies for attack and defense, and simulation-based risk management. These all have, as common threads, the notions that (1) the results of individual runs are less important than the aggregate results of many runs that tend to explore the space, and (2) relative results are meaningful while absolute results are even better.
We are then left with the second question of quality; the sensitivity of results to the accuracy of the values of simulation parameters. Clearly, wild parameter values will yield wild results, but without an extreme level of effort, reasonable parametric values can be attained by the solicitation of expert opinions and some examination and testing of the particulars of the organization and systems under analysis. This is the technique we use for generating metrics. The question of sensitivity can be addressed by varying parameters to different degrees and re-simulating to determine the effect on results. For parameters where changes within the tolerance of current measurement have significant impacts, accuracy is more important and measurements can be improved, while parameters that are relatively insensitive need not be so accurately determined. In this case, the simulation capability is itself a useful tool in determining sensitivity and the need for accuracy in parameters.
It turns out, however, that this issue is a bit tricker than this analysis might indicate, because of the scale of the issue. With between 35,000 and 40,000 parameters to consider, and with the statistical requirement of n^2 samples for accuracy of 1/n, even 10 percent accuracy requires 100 simulation runs per parameter value. Exercising 40,000 parameters over a range of 10 values then implies 40 million simulation runs just to determine sensitivity to each parameter varied one at a time. Parameters can conspire synergistically as well, leading to enormous numbers of simulation runs. This of course assumes that simulation results act like random stochastic processes, which they do not, because of the sequential nature of attack and defense. Our initial simulation runs appear to indicate that results do not change by more than a few percent after something like 1,000 runs per parameter set (stochastic analysis would predict a 3.33% deviation at 1,000 samples). If we were to use 1,000 runs, the variation of parameters analysis for each single parameter would take about 400 million runs.
While 400 million simulation runs is not unreasonable given the performance of the present simulator, (with a $500,000 parallel processor this can be done in only a few days) it turns out that we can generate significant sensitivity results for aggregate runs without the need to put forth this effort, and in the process learn a fair amount about the nature of the information protection design space for the particular situation under consideration. Indeed these results may be far more broadly applicable.
It turns out that the nature of the simulation space generated by the binary relation between (1) threat and attack and (2) attack and defense is such that there are only two possible values for these relations. While the simulation may be quite sensitive to these values, they are not subject to variations in parameters except over the values of true and false. Thus two cases exist for these values, which comprise about half of all the values used in the simulation. Furthermore, the vast majority of these values are well known and definitively resolved by the literature and theoretical or practical constraints. For example, we know definitively that locks are effective at preventing some portion of cable cuts, while authentication of packets is most certainly not effective in that role. The elimination of most of these parameters from sensitivity analysis reduces the level of effort by about half.
Perhaps the second most important thing to note in sensitivity analysis is that the times associated with attacks and defenses lead to sets of ordered events. Changes in the absolute values of times are of no import to the final outcome (win or lose) unless they change the ordering of events. Furthermore, many event sequences are only partially order dependent, so that many different orderings may result in equivalent outcomes. It turns out that time represents something like 1/3 of all of the parameters involved in simulation and that many of these times are also fixed against common standards - such as the organization's ability to respond or the limits of performance of current intrusion detection technology. Again, we know or can determine the values of many of these parameters with adequate accuracy so that variations do not have sufficient aggregate affect on the ordering of events so as to cause results to vary significantly for changes in value within our ability to reasonably measure them. This eliminates about another third of the values from the requirement for variation of parameter analysis.
While the results are impacted by changes in the remaining parameters, the impact is essentially linear in the values of those parameters because they are used in a linear fashion to affect outcomes. The net effect is that, except in cases where a win or loss is a close call decided by the value of a parameter, errors aren't magnified significantly by the process. In the case where close calls have an impact, there are two possible impacts; (1) the overall sequence of events is significantly impacted, or (2) the threshold between a win and a loss is changed by the value of the parameter.
In the case of the sequence of events being impacted, the impact can only effect a number of runs proportional to the variation in the parameter. In other words, the value of a metric associated with an attack or defense that works instead of failing in any given run, (or vice versa) impacts the set of all runs where that attack was tried linearly in the value of that metric. So a 10 percent increase in the value of the parameter has at most a 10 percent impact on outcomes of the steps in which it is exercised. Since there are about 100 attack methods and 150 defense methods and only one is selected for the next step at any given moment, in the aggregate, the effect of a 10 percent difference in the value of one parameter is significantly reduced by the likelihood that it will get selected (in the case of attack) or the impact on the attack (in the case of a defense). While variations may have significant impacts on a single run, their impact on a large number of runs is significantly lessened based on their import to the overall situation. In situations where defenses are not very resilient and where attackers are capable of only a few attack methods, the impact of minor changes is greater, because they effect a larger portion of the runs. This is a real-world effect of a lack of redundancy, not just a residual of the simulator, and just as the real world situation will be highly sensitive to minor changes in this circumstance, so will the simulator.
A specific example may be quite helpful here. Suppose that we have a situation where the differences between success and failure are within the bounds of the accuracy of our values. Such an example appears in one of the sample runs shown in Table 4 and is repeated here for the purpose of discussion:
What: ATTACK Node: Angel Time: 33d 1h 23m 30s What: infrastructure observation->Angel Details: [907 !< 866](21 > 20) -> bad luck
In this case, the details indicate that the defense missed preventing the attack by less than a 10 percent difference in the metric associated with its strength in this application (as indicated by the [907 !< 866]). The attack similarly failed because of a very small difference between the random number selected for this run and the overall strength of the attack in the situation (as indicated by the 21>20). If either had a 10 percent difference in values in the proper direction, the results would have been a prevention (in the case of the defense) or a successful attack (in the case of the attack). The net effect of the defensive failure in this simulation run was nothing because the attack failed due to bad luck anyway. The net effect on the attack for this simulation run was that Angel was not defeated until 73d 15h 16m into the run, about a 40 day difference. And yet the overall attack run achieved success at 136d 59m 10s, so that the total effect on attack time was 40 days out of 136 days - or about 30 percent. But this is not the whole story because - from later in that same simulation run we see this:
What: ATTACK Node: Charlie Time: 73d 19h 16m What: cryptanalysis->Charlie Details: [404 !< 0](19 < 20) =======> Prevention will fail
After Angel was penetrated, the attacker got lucky in the same type of close call (19<20) and defeated Charlie immediately. Who knows what might have happened next had this attack not succeeded? Again, a small variation in a parameter could have made the difference between immediate success and the attacker trying, for example, a strategic or tactical deception - an attack that would have taken 30 days of effort and may not have succeeded either.
Clearly, we cannot evaluate the results from such runs on a piecemeal basis because of the role that luck may play in attack and defense. Rather, because we cannot accurately measure the situations to the point of being able to be predictive on a case by case basis, we must consider them in the aggregate in order to derive meaningful results. If we think in these terms, it should be clear that a 10 percent difference in the value of the threshold used at any given point in a run will produce a 10 percent change in the number of times there is a success or failure at that point in the simulation. If a particular value is used repeatedly, the effect will accumulate in that run. The net effect will be a time difference in the outcomes of the runs, or in the case where detection and reaction are taken into consideration, an increase or decrease in the wins or losses. Since there are many such events in a typical run, each of which could have an effect in either direction, random errors tend to cancel while correlated errors tend to compliment each other. This is what we see, for example, in the analysis of defender strength and reaction time for the large numbers of sample runs shown in Plates 3 and 6.
The aggregate results provide us with information on the shapes of the curves, but clearly, sensitivity depends on where you are on these curves. For example, in Plate 11 (Instant Reaction Total Expected Loss vs. Defender Strength) small errors in defender strength near 100 percent make little difference as will small changes at very low defender strength, but changes between 30 percent and 60 percent cover more than a factor of 3 in expected loss. The ability to measure accurately is far more important if we intend to operate in the middle portion of the curve, while the ability to measure is far less important near the minimums and maximums. If we add an equation for defender strength vs. investment defender strength (i.e., via education and skills development) the place where the sum of the cost of defenders and the expected loss are minimized provides the optimum for costs of training vs. expected loss, and the sensitivity around that point is the issue that has to be settled to better optimize this investment.
The same sort of analysis will apply to other parameters of interest such as reaction time. This would seem to suggest an iterative process wherein initial values that are reasonably accurate are used, simulations are done to analyze tradeoffs, and where decisions must be made near highly sensitive areas of curves, more detailed data is measured and more simulations are run in close proximity to the decision point. This notion of variable granularity is not unique to information protection simulation, nor is the idea of using an iterative process for getting the desired accuracy.
Finally, we have the issue of how we obtain data that is appropriately accurate. We begin the iterative process with an initial set of values and an initial model of the network under consideration. We use a gathering process that involves a great deal of expert opinion combined with selective experiments or demonstrations. But if the initial data is not accurate, we may not know whether we are in a sensitive or insensitive portion of the analysis. In other words, without accurate data, we cannot accurately tell whether we need more accurate data or not.
In the end, ground truth can only be measured in the real world. While simulation can help us analyze and improve experimental results, it does not eliminate the need for them both as a basis for simulation and for its validation.
This leads us directly to the question of validation. Let us suppose that our ordinal basis is simply wrong and that our model of threats, attack mechanisms, and defensive measures is not reflective of the reality of attack and defense. In this case, the results of simulation are essentially useless. Similarly, if our model of sequential attacks or strategies is invalid, the results are far less predictive than would be desired. If our metrics of time and strength are not reflective of reality, our results will be far less accurate than desired, and again we will lose predictive power. Validation is needed in order to be able to determine whether or not these issues are being properly addressed and how predictive the results might be.
The scientific method generally uses a process that begins with theory, produces a model, performs experiments based on the model to confirm or refute the theory, and feeds back the results to confirm or refute the theory. As a meta-issue, we will assume that the schema of the scientific method as described here is valid. We then need to perform validation by creating a theory, model, experimental regime, set of experiments, and analysis.
The theory behind our simulation and the specific set of threats, attack mechanisms, and defense mechanisms are those of espoused in "Preliminary Classification Scheme for Information System Threats, Attacks, and Defenses; A Cause and Effect Model; and Some Analysis Based on That Model" [Cohen98] In essence, we posit that causes produce effects through mechanisms. We model this theory with the cause and effect model shown in Plate 1 consisting of threats which use attack mechanisms to cause effects and defenses which mitigate effects by mitigating threats, the links between threats and attack mechanisms, attack mechanisms, the links between attack mechanisms and consequences, and/or consequences.
As was discussed earlier, experiments can be quite expensive and this limits our ability to carry them out. As an alternative, we use a combination of historical data, expert opinion, and limited experiments to try to generate results that are viable for validation.
Historical data, while limited, tends to support the general notions underlying the model in the sense that accounts of attacks as they occur tend to reflect sequences of activities of the sorts produced by our model. This has been validated by examination of the model and select runs of the simulator by many active researchers and practitioners as well as by a substantial review of the literature.
Expert opinion, including the experiences of investigators who have field experience with scores of cases and consultants who regularly work in the field, tend to support the notion that the models are valid and, to a limited extent, that the linkages between threats, attacks mechanisms, and defensive mechanisms are also valid. While there is certainly no consensus of opinion on the particular scheme we use there are also few who dispute that, to the extent that it models the reality of cyber attack and defense, it models it reasonably well.
Limited experiments have also been performed to validate some of the specific numbers and results from published papers and comparisons of products form the basis for many of the numerical values used as metrics. Details of some of the values used in our simulator are provided in the references. [Cohen9903]
Perhaps the least compelling but most important validation of the simulation system is the opinions of people who run individual simulations. In essence, they indicate that the sequences of events and the things that transpire seem reasonable to them. If the results did not seem reasonable, it would be cause for great concern and would be considered a serious refutation. And yet this sort of opinion does little to give us confidence in these results. A further complicaiton comes from the fact that environments differ considerably, so that time-related information, especially in the area of response times, is hard to validate without individual experiments and testing of the specific organization under realistic circumstances.
Perhaps the most compelling results to date are those presented in this paper on issues related to the value of faster reaction, skill levels of defenders, and so forth. When we inspect the specific runs for deeper understanding of why a phenomenon exists, we always seem to find a reasonable explanation that, while sometime surprising, makes sense once we investigate it. This ability of simulation to resolve what would otherwise be rank speculation and to do so in surprising but sensible ways is its greatest validation to date. This indicates not only that the simulations make sense, but that the aggregate results are meaningful in the same way as experiments, even if only at a qualitative level. Indeed, the results appear to have meaning at a quantitative level as well, but this depends heavily on our ability to gather data about the specific circumstance under consideration.
In the long run, widespread use of simulation will produce validation in the form of real-world experience that confirms or refutes the simulation results. For the meanwhile, we are limited in our ability to validate results.
We have presented a great deal of information on the application of modeling and simulation technologies to information protection, but there is clearly a long way to go.
We have presented information on modeling approaches and discussed the reasons for our choice of models, briefly described the operation of a simulation engine, and shown sample detailed output runs from simulations to give a sense of what precisely is simulated and what sort of results are derived.
Perhaps the most interesting results here are the shapes of the outcome curves over time and the association of this phenomena with the high degree of time gradation between different attack methods. This result has many implications and, while it may seem almost obvious once it is presented, it was unpublished and not known to the author until simulations revealed it, and it was a surprise until the detailed simulation results were examined. This has all of the hallmarks of a valid experimental basis for scientific inquiry.
Parallel simulation was described from a technology standpoint and the results of parallel simulations yielded intriguing results. While parallelism attained in our experiments was relatively poor, we believe that almost ideally scalable parallelism is attainable for these simulations. The effect of parallelism in this sort of simulation is most dramatic in that it enables analyses that would otherwise be impractical.
The curves derived for the effects of defender strength, success rates, and threats and the non-linear shape of those curves were particularly revealing as were the results on the effects of reaction time on success rates. To our knowledge these sorts of results have never been demonstrated before, and they are particularly interesting because of their combination with the results on dead zones in attack times.
By adding costs into the analysis, we were able to demonstrate non-linearities in the tradeoff between skills of defenders and reduction in expected loss, and perhaps the most important result here was that it is not cost effective to have the best computer security experts in an active defense role. For a reasonable cost, we can likely train existing employees to provide the most cost effective reaction capability.
Finally, we discussed issues of metrics, sensitivity, and validation - a key component of any simulation-based technology. The most important result here is that, for the purposes we are currently applying simulations to address, accuracy does not have to be very good in order to learn a lot more than we know now. At the same time, the data requirements for accurate simulation are substantial and represent a level of effort only well suited today to large organizations with considerable assets at risk.
It appears that these initial results are only the beginning of the sorts of results that simulation technology will provide in the information protection field, and that it is a fruitful area to explore.